Câu hỏi
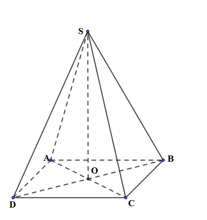
Cho hình chóp tứ giác đều \(S.ABCD\) có cạnh đáy bằng \(a\sqrt 3 \), góc \(\widehat {ASB} = {60^0}\). Tính thể tích của khối nón đỉnh \(S\) có đáy là đường tròn ngoại tiếp tứ giác \(ABCD\).
- A \(\frac{{\pi {a^3}\sqrt 6 }}{8}\).
- B \(\frac{{\pi {a^3}\sqrt 6 }}{4}\).
- C \(\frac{{\pi {a^3}\sqrt 6 }}{{12}}\).
- D \(\frac{{\pi {a^3}\sqrt 6 }}{2}\).
Phương pháp giải:
\({V_{non}} = \frac{1}{3}\pi {R^2}h\)
Lời giải chi tiết:
\(S.ABCD\) là chóp tứ giác đều \( \Rightarrow ABCD\) là hình vuông
\( \Rightarrow BD = AB\sqrt 2 = a\sqrt 3 .\sqrt 2 = a\sqrt 6 \Rightarrow r = OB = \frac{{BD}}{2} = \frac{{a\sqrt 6 }}{2}\)
Tam giác SAB có: \(SA = SB,\,\,\widehat {ASB} = {60^0} \Rightarrow \Delta SAB\) đều \( \Rightarrow SA = AB = a\sqrt 3 \)
\( \Rightarrow SB = SD = AD = AB = a\sqrt 3 \)
\( \Rightarrow \Delta SBD = \Delta ABD\,\,\left( {c.c.c} \right) \Rightarrow SO = OA = OB = OD = \frac{{a\sqrt 6 }}{2}\)
Thể tích của khối nón đỉnh \(S\) có đáy là đường tròn ngoại tiếp tứ giác \(ABCD\):
\(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi .O{A^2}.SO = \frac{1}{3}\pi .{\left( {\frac{{a\sqrt 6 }}{2}} \right)^3} = \frac{{\pi {a^3}\sqrt 6 }}{4}\) .
Chọn: B