Phương pháp giải:

+) Đặt \(t = \sqrt {2x - 3} \,\,\left( {t \ge 0} \right)\), rút x theo t.

+) Thế vào phương trình, lập phương hai vế, cô lập m, đưa phương trình về dạng \(m = f\left( t \right)\).

+) Khảo sát và lập BBT của hàm số \(y = f\left( t \right)\,\,\left( {t \ge 0} \right)\). Biện luận để phương trình có 2 nghiệm phân biệt.

Lời giải chi tiết:

Đặt \(\sqrt {2x - 3}  = t,\,\left( {t \ge 0} \right)\) \( \Rightarrow x = \frac{{{t^2} + 3}}{2}\) . Phương trình trở thành:

\(\begin{array}{l}\sqrt[3]{{m - \frac{{{t^2} + 3}}{2}}} + t = 4 \Leftrightarrow \sqrt[3]{{m - \frac{{{t^2} + 3}}{2}}} = 4 - t \Leftrightarrow m - \frac{{{t^2} + 3}}{2} = {\left( {4 - t} \right)^3}\\ \Leftrightarrow m = \frac{{{t^2} + 3}}{2} + {\left( {4 - t} \right)^3} \Leftrightarrow m = \frac{{{t^2}}}{2} + \frac{3}{2} + 64 - 48t + 12{t^2} - {t^3} \Leftrightarrow m =  - {t^3} + \frac{{25}}{2}{t^2} - 48t + \frac{{131}}{2}\end{array}\)

Xét hàm số \(y = f\left( t \right) =  - {t^3} + \frac{{25}}{2}{t^2} - 48t + \frac{{131}}{2},\,\,t \ge 0\) ta có: \(f'(t) =  - 3{t^2} + 25t - 48 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 3\\t = \frac{{16}}{3}\end{array} \right.\)

Bảng biến thiên:

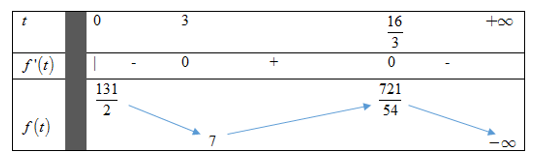
Để phương trình có 3 nghiệm phân biệt \(\,t \ge 0\) thì \(7 < m < \frac{{721}}{{54}}\) \( \Rightarrow m \in \left\{ {8;9;10;11;12;13} \right\}\)

\( \Rightarrow \) Có 6 giá trị nguyên của m thỏa mãn.

Chọn: B