Câu hỏi
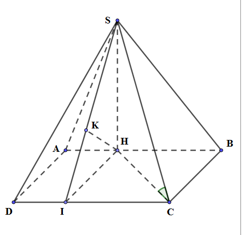
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, \(AB = a,\,AD = \sqrt 2 a\), góc giữa hai mặt phẳng (SAC) và (ABCD) bằng \({60^0}\). Gọi H là trung điểm của AB. Biết rằng tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính theo a bán kính mặt cầu ngoại tiếp hình chóp S.HAC.
- A \(\frac{{9\sqrt 2 a}}{8}\).
- B \(\frac{{\sqrt {62} a}}{{16}}\).
- C \(\frac{{\sqrt {62} a}}{8}\).
- D \(\frac{{\sqrt {31} a}}{{32}}\).
Phương pháp giải:
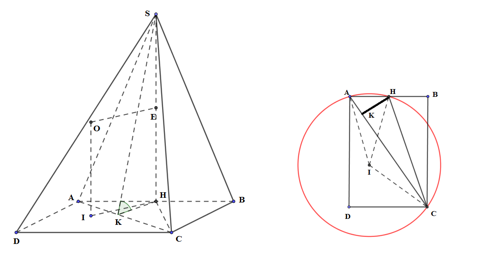
+) Gọi I là tâm đường tròn ngoại tiếp tam giác AHC và E là trung điểm của BC.
+) Qua I dựng đường thẳng song song với SH, qua E dựng đường thẳng song song với IH, hai đường thẳng này cắt nhau tại O \( \Rightarrow O\) là tâm mặt cầu ngoại tiếp chóp S.AHC.
+) Tính IH, sử dụng công thức \(R = \frac{{abc}}{{4S}}\) với a, b, c là ba cạnh của tam giác AHC, S là diện tích tam giác AHC, R là bán kính đường tròn ngoại tiếp tam giác AHC.
+) Tính HE.
+) Sử dụng định lí Pytago tính OH.
Lời giải chi tiết:
Kẻ HK vuông góc AB tại K, gọi I là tâm đường tròn ngoại tiếp tam giác AHC, E là trung điểm của SH.
Ta có: H là trung điểm của AB, tam giác SAB cân tại S \( \Rightarrow SH \bot AB\)
Mà SAB nằm trong mặt phẳng vuông góc với đáy \( \Rightarrow SH \bot \left( {ABCD} \right)\)
\(\Delta AHK\) đồng dạng \(\Delta ACB\,\,\left( {g.g} \right)\)
\( \Rightarrow \frac{{AH}}{{AC}} = \frac{{HK}}{{BC}} \Leftrightarrow \frac{{\frac{a}{2}}}{{\sqrt {{a^2} + {{\left( {\sqrt 2 a} \right)}^2}} }} = \frac{{HK}}{{\sqrt 2 a}} \Leftrightarrow HK = \frac{a}{{\sqrt 6 }}\)
Ta có: \(HK \bot AC,\,\,SH \bot AC \Rightarrow AC \bot \left( {SHK} \right) \Rightarrow AC \bot SK\)
\( \Rightarrow \widehat {\left( {\left( {SAC} \right);\left( {ABCD} \right)} \right)} = \widehat {SKH} = {60^0}\)
\(\Delta SKH\) vuông tại H, \(\widehat {SKH} = {60^0} \Rightarrow SH = HK.\tan {60^0} = \frac{a}{{\sqrt 6 }}.\sqrt 3 = \frac{a}{{\sqrt 2 }}\)\( \Rightarrow EH = \frac{a}{{2\sqrt 2 }}\)
Ta có: \({S_{\Delta AHC}} = \frac{1}{2}{S_{\Delta ABC}} = \frac{1}{2}.\frac{1}{2}.{S_{ABCD}} = \frac{{{S_{ABCD}}}}{4} = \frac{{{a^2}\sqrt 2 }}{4}\)
I là tâm đường tròn ngoại tiếp tam giác AHB
\( \Rightarrow IH = R = \frac{{AH.HC.AC}}{{4{S_{\Delta AHC}}}} = \frac{{\frac{a}{2}.\sqrt {{{\left( {\frac{a}{2}} \right)}^2} + {{\left( {\sqrt 2 a} \right)}^2}} .\sqrt {{a^2} + {{\left( {\sqrt 2 a} \right)}^2}} }}{{4.\frac{{{a^2}\sqrt 2 }}{4}}} = \frac{{\frac{a}{2}.\frac{{3a}}{2}.\sqrt 3 a}}{{{a^2}\sqrt 2 }} = \frac{{3\sqrt 3 a}}{{4\sqrt 2 }}\)
Tứ giác OEHI là hình chữ nhật \( \Rightarrow OH = \sqrt {I{H^2} + E{H^2}} = \sqrt {{{\left( {\frac{{3\sqrt 3 a}}{{4\sqrt 2 }}} \right)}^2} + {{\left( {\frac{a}{{2\sqrt 2 }}} \right)}^2}} = \sqrt {\frac{{27{a^2}}}{{32}} + \frac{{{a^2}}}{8}} = \frac{{\sqrt {62} a}}{8}\)
Vậy, bán kính mặt cầu ngoại tiếp hình chóp S.HAC là \(\frac{{\sqrt {62} a}}{8}\).
Chọn: C