Phương pháp giải:

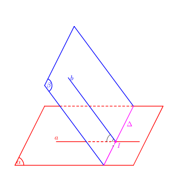
Xác định góc giữa hai mặt phẳng \(\left( \alpha  \right),\,\,\left( \beta  \right)\):

- Tìm giao tuyến \(\Delta \) của \(\left( \alpha  \right),\,\,\left( \beta  \right)\).

- Xác định 1 mặt phẳng \(\left( \gamma  \right) \bot \Delta \).

- Tìm các giao tuyến \(a = \left( \alpha  \right) \cap \left( \gamma  \right),b = \left( \beta  \right) \cap \left( \gamma  \right)\)

- Góc giữa hai mặt phẳng \(\left( \alpha  \right),\,\,\left( \beta  \right)\): \(\widehat {\left( {\left( \alpha  \right);\left( \beta  \right)} \right)} = \widehat {\left( {a;b} \right)}\).

Lời giải chi tiết:

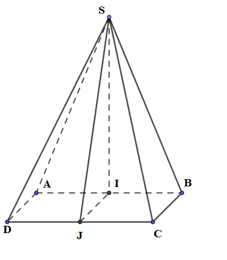
Gọi I, J lần lượt là trung điểm của AB, CD.

Tam giác SAB cân tại S \( \Rightarrow SI \bot AB\)

Vì mặt bên SAB  nằm trong mặt phẳng vuông góc với (ABCD) nên \(SI \bot \left( {ABCD} \right)\)

Ta có: \(IJ \bot CD,\,\,SI \bot CD \Rightarrow CD \bot (SIJ)\)

\(\left\{ \begin{array}{l}\left( {SCD} \right) \cap \left( {ABCD} \right) = CD\\\left( {SIJ} \right) \bot CD\\\left( {SIJ} \right) \cap \left( {SCD} \right) = SJ\\\left( {SIJ} \right) \cap \left( {ABCD} \right) = IJ\end{array} \right.\,\, \Rightarrow \widehat {\left( {SCD} \right);\left( {ABCD} \right)} = \widehat {\left( {SJ;IJ} \right)} = \widehat {SJI}\,\,\left( {do\,\,\widehat {SJI} < {{90}^0}} \right)\)

 \(\begin{array}{l}\,\,\,\,\,\cos \widehat {SJI} = \frac{{2\sqrt {19} }}{{19}}\\ \Rightarrow \frac{{IJ}}{{SJ}} = \frac{{2\sqrt {19} }}{{19}} \Rightarrow SJ = \frac{a}{{\frac{{2\sqrt {19} }}{{19}}}} = \frac{{a\sqrt {19} }}{2}\\ \Rightarrow SI = \sqrt {S{J^2} - I{J^2}}  = \sqrt {{{\left( {\frac{{a\sqrt {19} }}{2}} \right)}^2} - {a^2}}  = \frac{{a\sqrt {15} }}{2}\end{array}\)

Thể tích của khối chóp  S.ABCD: \(V = \frac{1}{3}.SI.{S_{ABCD}} = \frac{1}{3}.\frac{{a\sqrt {15} }}{2}.{a^2} = \frac{{{a^3}\sqrt {15} }}{6}\).

Chọn: B