Phương pháp giải:

- Tìm TXĐ

- Tính y’

- Lập bảng biến thiên của hàm số trên đoạn \(\left[ { - 1;\frac{1}{2}} \right]\)

- Xác định giá trị lớn nhất và giá trị nhỏ nhất của hàm số

- Tính tích M.m.

Lời giải chi tiết:

TXĐ: \(D = R{\rm{\backslash }}\left\{ 1 \right\}\)

\(y = \frac{{{x^2} - 3x + 3}}{{x - 1}} \Rightarrow y' = \frac{{\left( {2x - 3} \right)\left( {x - 1} \right) - 1.\left( {{x^2} - 3x + 3} \right)}}{{{{\left( {x - 1} \right)}^2}}} = \frac{{{x^2} - 2x}}{{{{\left( {x - 1} \right)}^2}}}\)

\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\)

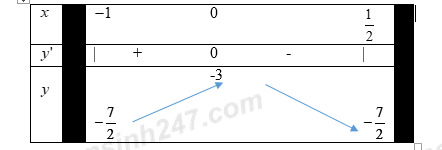
Bảng biến thiên trên đoạn \(\left[ { - 1;\frac{1}{2}} \right]\):

Giá trị nhỏ nhất \(m =  - \frac{7}{2}\), giá trị lớn nhất \(M =  - 3\) \( \Rightarrow M.m = \frac{{21}}{2}\).

Chọn: C