Câu hỏi
Có 4 nữ tên là: Huệ, Hồng, Lan, Hương và 4 nam tên là An, Bình, Hạnh, Phúc cùng ngồi quanh một bàn tròn có 8 chỗ.
a) Hỏi có bao nhiêu cách sắp xếp biết nam và nữ ngồi xen kẽ nhau?
b) Hỏi có bao nhiêu cách sắp xếp biết nam và nữ ngồi xen kẽ nhau nhưng bạn Hồng và An không chịu ngồi cạnh nhau?
- A a) 144; b) 72
- B a) 156; b) 72
- C a) 156; b) 69
- D a) 144; b) 69
Lời giải chi tiết:
a)
+) Ta xếp 4 bạn nam trước: Vậy có 4! Cách.
+) Khi xếp xong, giữa 2 bạn nam có 1 khoảng trống, chọn 4 bạn nữ xếp vào 4 khoảng trống đó là 4! Cách.
+) Vì đây là bàn tròn, hơn nữa vai trò 4 bạn nam là như nhau nên sẽ có 4 cách trùng lặp (do các vị trí đối xứng nhau của bàn tròn – hoặc khi xoay bàn tròn)
+) Vậy có: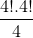 
= 144 cách sắp xếp
b)
+) Trước hết nếu ta xếp 2 bạn Hồng và An ngồi cạnh nhau sẽ có 2 cách xếp
+) Chọn 3 bạn nam còn lại xếp vào 3 vị trí có 3! Cách
+) Chọn 3 bạn nữ xếp vào 3 vị trí xen kẽ có 3! Cách
Vậy nếu xếp xen kẽ nhưng Hồng và An luôn ngồi cạnh nhau sẽ có 2.3!.3! = 72 cách
Kết luận: Số cách xếp xen kẽ mà Hồng và An không ngồi cạnh nhau là: 144 – 72 = 72 cách
Câu hỏi trước
