Câu hỏi
Từ 5 chữ số 1; 2; 3; 4; 5 có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số khác nhau, trong đó có bao nhiêu số lẻ, bao nhiêu số không chia hết cho 5?
- A 120; 72; 69
- B 120; 72; 96
- C 120; 84; 69
- D 120; 84; 96
Lời giải chi tiết:
+) Ta có: P5 = 5! = 120 số tự nhiên có 5 chữ số khác nhau
+) Gọi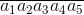 
là số tự nhiên lẻ có 5 chữ số khác nhau được lập từ các chữ số 1; 2; 3; 4; 5. Để số cần tìm là số lẻ thì
Khi đó a5 
{1; 3; 5} nên có 3 cách chọn, 4 số còn lại có 4! Cách chọn
Vậy có: 3.4! = 72 số tự nhiên lẻ có 5 chữ số khác nhau được lập từ các chữ số 1; 2; 3; 4; 5
+) Gọi 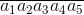là số tự nhiên chia hết cho 5 có 5 chữ số khác nhau được lập từ các chữ số 1; 2; 3; 4; 5
Khi đó a5 = 5 nên có 1 cách chọn, 4 số còn lại có 4! Cách chọn.
Vậy có 1.4! = 24 số tự nhiên chia hết cho 5 có 5 chữ số khác nhau được lập từ các chữ số 1; 2; 3; 4; 5
Như vậy có 120 - 24 = 96 số tự nhiên có 5 chữ số không chia hết cho 5
