Câu hỏi
Cho tam giác ABC. Gọi I, J, K lần lượt là trung điểm của BC, CA, AB. Điểm M thỏa mãn: \(2\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \) . M trùng với :
- A Điểm I
- B Trung điểm của AJ.
- C Trung điểm của KJ.
- D Tâm hình bình hành BKIJ.
Lời giải chi tiết:
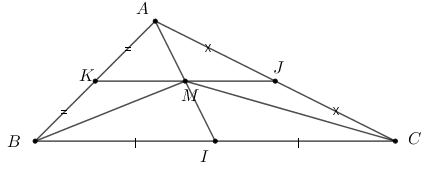
Từ đề bài ta có:
\(\begin{array}{l}2\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \\ \Rightarrow \left( {\overrightarrow {MA} + \overrightarrow {MB} } \right) + \left( {\overrightarrow {MA} + \overrightarrow {MC} } \right) = \overrightarrow 0 \\ \Rightarrow 2\overrightarrow {MK} + 2\overrightarrow {MJ} = \overrightarrow 0 \\ \Rightarrow \overrightarrow {MK} = - \overrightarrow {MJ} \end{array}\)
Khi đó M là trung điểm của KJ.
Chọn C.
Câu hỏi trước
