Lời giải chi tiết:

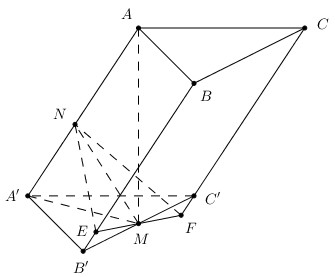
Qua M dựng mặt phẳng (P) vuông góc với AA’ cắt các cạnh AA’; BB’; CC’ lần lượt tại N, E, F.

Ta có \(\left\{ \begin{array}{l}AA' \bot NE \Rightarrow NE = d\left( {E;AA'} \right) = d\left( {N;BB'} \right) = d\left( {A;BB'} \right) = 1\\AA' \bot NF \Rightarrow NF = d\left( {F;AA'} \right) = d\left( {N;CC'} \right) = d\left( {A;CC'} \right) = \sqrt 3 \\AA' \bot \left( P \right) \Rightarrow CC' \bot \left( P \right) \Rightarrow CC' \bot EF \Rightarrow EF = d\left( {E;CC'} \right) = d\left( {F;BB'} \right) = d\left( {C;BB'} \right) = 2\end{array} \right.\)

\( \Rightarrow \Delta NEF\) vuông tại N (Định lí Pytago đảo)

Lại có \(\dfrac{{ME}}{{MF}} = \dfrac{{MB'}}{{MC'}} = 1 \Rightarrow ME = MF\) (định lí Ta-lét) \( \Rightarrow M\) là trung điểm của EF.

 \( \Rightarrow MN = \dfrac{1}{2}EF = 1\)

Xét tam giác vuông AA’M có: \(\dfrac{1}{{M{N^2}}} = \dfrac{1}{{A{M^2}}} + \dfrac{1}{{A'{M^2}}} \Rightarrow 1 = \dfrac{1}{{A{M^2}}} + \dfrac{1}{4} \Rightarrow AM = \dfrac{2}{{\sqrt 3 }}\)

Ta có \(\left\{ \begin{array}{l}\left( P \right) \bot AA'\\\left( {A'B'C'} \right) \bot AM\end{array} \right. \Rightarrow \widehat {\left( {\left( P \right);\left( {A'B'C'} \right)} \right)} = \widehat {\left( {AA';AM} \right)} = \widehat {A'MA}\)

\(\cos \widehat {A'MA} = \dfrac{{AM}}{{AA'}} = \dfrac{{\dfrac{2}{{\sqrt 3 }}}}{{\sqrt {\dfrac{4}{3} + 4} }} = \dfrac{1}{2}\)

Dễ thấy tam giác NEF là hình chiếu vuông góc của \(\Delta A'B'C'\) lên mặt phẳng (P)

\( \Rightarrow {S_{\Delta A'B'C'}} = \dfrac{{{S_{\Delta NEF}}}}{{\cos \widehat {A'MA}}} = \dfrac{{\dfrac{1}{2}NE.NF}}{{\dfrac{1}{2}}} = 1.\sqrt 3  = \sqrt 3 \)

Vậy thể tích khối lăng trụ là \(V = AM.{S_{\Delta A'B'C'}} = \dfrac{2}{{\sqrt 3 }}.\sqrt 3  = 2\)

Chọn B.