Câu hỏi
Cho hai hàm số \(y = f\left( x \right),y = g\left( x \right)\). Hai hàm số \(y = f'\left( x \right),y = g'\left( x \right)\)có đồ thị như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số \(y = g'\left( x \right)\). Hàm số \(h\left( x \right) = f\left( {x + 3} \right) - g\left( {2x - \dfrac{7}{2}} \right)\) đồng biến trên khoảng nào dưới đây ?
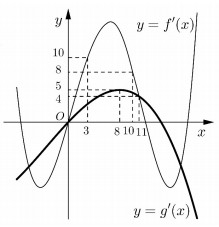
- A \(\left( {\dfrac{{13}}{4};4} \right)\)
- B \(\left( {7;\dfrac{{29}}{4}} \right)\)
- C \(\left( {6;\dfrac{{36}}{5}} \right)\)
- D \(\left( {\dfrac{{36}}{5}; + \infty } \right)\)
Phương pháp giải:
Giải bất phương trình \(h'\left( x \right) > 0\).
Lời giải chi tiết:
Ta có: \(h'\left( x \right) = f'\left( {x + 3} \right) - 2g'\left( {2x - \frac{7}{2}} \right)\)
Để hàm số đồng biến trên
\(\begin{array}{l}\left( {a;b} \right) \Rightarrow h'\left( x \right) > 0\,\,\forall x \in \left( {a;b} \right) \Rightarrow f'\left( {x + 3} \right) > 2g'\left( {2x - \frac{7}{2}} \right)\,\,\forall x \in \left( {a;b} \right)\\ \Rightarrow \mathop {\min }\limits_{\left( {a;b} \right)} f'\left( {x + 3} \right) > 2\mathop {\max }\limits_{\left( {a;b} \right)} g'\left( {2x - \frac{7}{2}} \right)\end{array}\)
\(\begin{array}{l}x \in \left( {\dfrac{{13}}{4};4} \right) \Rightarrow \left\{ \begin{array}{l}x + 3 \in \left( {\dfrac{{25}}{4};7} \right) \Rightarrow f'\left( {x + 3} \right) > 10 \Rightarrow \mathop {\min }\limits_{\left( {\dfrac{{13}}{4};6} \right)} f'\left( {x + 3} \right) > 10\\2x - \dfrac{7}{2} \in \left( {3;\dfrac{9}{2}} \right) \Rightarrow g'\left( {2x - \dfrac{7}{2}} \right) < 5 \Rightarrow 2\mathop {\max }\limits_{\left( {a;b} \right)} g'\left( {2x - \dfrac{7}{2}} \right) < 10\end{array} \right.\\ \Rightarrow \mathop {\min }\limits_{\left( {a;b} \right)} f'\left( {x + 3} \right) > 2\mathop {\max }\limits_{\left( {a;b} \right)} g'\left( {2x - \dfrac{7}{2}} \right)\end{array}\)
\( \Rightarrow \) Hàm số \(y = h\left( x \right)\) đồng biến trên \(\left( {\dfrac{{13}}{4};4} \right)\).
Chọn A.







