Câu hỏi
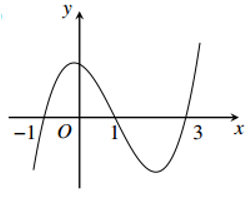
Cho hàm số \(y = f\left( x \right)\). Hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ. Hàm số \(g\left( x \right) = f\left( {{x^2} - 1} \right)\) đồng biến trên khoảng nào dưới đây ?
- A \(\left( 1;+\infty \right)\)
- B \(\left( 1;2 \right)\)
- C \(\left( 0;1 \right)\)
- D \(\left( -2;-1 \right)\)
Phương pháp giải:
Dựa vào đồ thị hàm số \(y=f'\left( x \right)\) để xét dấu \(g'\left( x \right)=2x.f'\left( {{x}^{2}}-1 \right)\)
Lời giải chi tiết:
Xét với x thuộc ( 0 ; 1 ) ta có \(\) \(f'\left( 0-1 \right)<f'\left( {{x}^{2}}-1 \right)<f'\left( 1-1 \right)\)
Từ đồ thị hàm số \(y=f'\left( x \right)\) suy ra \(f'\left( {{x}^{2}}-1 \right)>0\)
Suy ra \(g'\left( x \right)=2x.f'\left( {{x}^{2}}-1 \right)>0\)
Suy ra hàm số \(g\left( x \right)\) đồng biến trên khoảng ( 0 ; 1 )
Chọn đáp án C