Câu hỏi
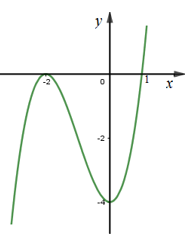
Cho hàm số \(y=f(x)\). Hàm số \(y=f'(x)\) là hàm số bậc ba có đồ thị như hình vẽ. Hàm số \(g(x)=f\left( -{{x}^{2}}+3 \right)\). Mệnh đề nào dưới đây đúng?
- A g(x) đồng biến trên khoảng\(\left( -\infty ;-\sqrt{2} \right)\).
- B g(x) đồng biến trên khoảng\(\left( 0;\sqrt{5} \right)\).
- C g(x) đồng biến trên khoảng\(\left( -\sqrt{2};0 \right)\).
- D g(x) nghịch biến trên khoảng\(\left( \sqrt{2};\infty \right)\).
Phương pháp giải:
Xét dấu \(g'(x)\) thông qua dấu của \(f'(x)\). Từ đó đánh giá khoảng đồng biến, nghịch biến của hàm số \(y=g(x)\).
Lời giải chi tiết:
\(g(x)=f\left( -{{x}^{2}}+3 \right)\Rightarrow g'(x)=-2x.f'\left( -{{x}^{2}}+3 \right)\)
\(f'\left( { - {x^2} + 3} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}
- {x^2} + 3 = - 2\\
- {x^2} + 3 = 1
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
{x^2} = 5\\
{x^2} = 2
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
x = \pm \sqrt 5 \\
x = \pm \sqrt 2
\end{array} \right.\)
Bảng xét dấu: 
\(\Rightarrow \) g(x) đồng biến trên khoảng\(\left( -\sqrt{2};0 \right)\) và \(\left( \sqrt{2};\sqrt{5} \right)\).
Chọn: C
Câu hỏi trước
