Câu hỏi
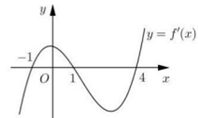
Cho hàm số \(y=f\left( x \right)\) liên tục và có đạo hàm trên R. Biết hàm số \(y=f'\left( x \right)\) có đồ thị như hình vẽ sau:
Hỏi hàm số \(y=f\left( 1-x \right)\) đồng biến trên khoảng nào?
- A \(\left( -1;1 \right)\) và \(\left( 4;+\infty \right)\)
- B \(\left( -3;0 \right)\) và \(\left( 2;+\infty \right)\)
- C \(\left( -\infty ;-1 \right)\) và \(\left( 1;4 \right)\)
- D \(\left( -4;-1 \right)\) và \(\left( 1;+\infty \right)\)
Phương pháp giải:
Giải bất phương trình \(y'>0\)
Lời giải chi tiết:
\(y'=-f'\left( 1-x \right)\)
Với \(x\in \left( -3;0 \right)\Rightarrow 1-x\in \left( 1;4 \right)\Rightarrow f'\left( 1-x \right)<0\Rightarrow y'>0\Rightarrow \) Hàm số đồng biến trên \(\left( -3;0 \right)\)
Với \(x\in \left( 2;+\infty \right)\Leftrightarrow \left( 1-x \right)\in \left( -\infty ;-1 \right)\Rightarrow f'\left( 1-x \right)<0\Rightarrow y'>0\Rightarrow \) Hàm số đồng biến trên\(\left( 2;+\infty \right)\)
Vậy hàm số đồng biến trên \(\left( -3;0 \right)\) và \(\left( 2;+\infty \right)\)
Chọn B.