Lời giải chi tiết:

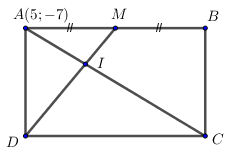
* Tìm C :

Giả sử \(C\left( {a;b} \right).\,\,C \in \left( \Delta  \right) \Rightarrow a - b + 4 = 0\,\,\left( 1 \right)\)

Nối \(AC \cap DM = I\). Vì \(CD = 2AM \Rightarrow IC = 2IA \Rightarrow \overrightarrow {IC}  =  - 2\overrightarrow {IA} \)

\(\begin{array}{l} \Rightarrow \left( {a - {x_I};b - {y_I}} \right) =  - 2\left( {5 - {x_I}; - 7 - {y_I}} \right)\\ \Rightarrow I\left( {\frac{{a + 10}}{3};\frac{{b - 14}}{3}} \right)\\I \in DM \Rightarrow 3a - 4b + 17 = 0\,\,\left( 2 \right)\end{array}\)

Giải hệ \(\left\{ \begin{array}{l}\left( 1 \right)\\\left( 2 \right)\end{array} \right. \Rightarrow C\left( {1;5} \right)\).

* Tìm B.

Giả sử \(B\left( {c;d} \right) \Rightarrow M\left( {\frac{{5 + c}}{2};\frac{{ - 7 + d}}{2}} \right)\)

\(M \in DM \Rightarrow 3c - 4d - 3 = 0\,\,\,\left( 3 \right)\)

\(\begin{array}{l}\left\{ \begin{array}{l}\overrightarrow {AB}  = \left( {c - 5;d + 7} \right)\\\overrightarrow {CB}  = \left( {c - 1;d - 5} \right)\end{array} \right.\\\overrightarrow {AB} .\overrightarrow {CB}  = 0 \Rightarrow \left( {c - 5} \right)\left( {c - 1} \right) + \left( {d + 7} \right)\left( {d - 5} \right) = 0\,\,\left( 4 \right)\end{array}\)

Giải hệ \(\left\{ \begin{array}{l}\left( 3 \right)\\\left( 4 \right)\end{array} \right. \Rightarrow \left\{ \begin{array}{l}B\left( { - 3; - 3} \right)\,\,\,\left( {tm} \right)\\B\left( {\frac{{33}}{5};\frac{{21}}{5}} \right)\,\,\left( {ktm} \right)\end{array} \right.\)