Câu hỏi
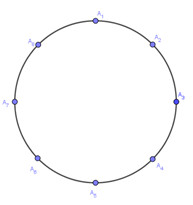
Có 8 bạn cùng ngồi xung quanh một cái bàn tròn, mỗi bạn cầm 1 đồng xu như nhau. Tất cả 8 bạn cùng tung đồng xu của mình, bạn có đồng xu ngửa thì đứng, bạn có đồng xu sấp thì ngồi. Xác suất để không có hai bạn liền kề cùng đứng là:
- A \(\frac{{47}}{{256}}\).
- B \(\frac{{49}}{{256}}\).
- C \(\frac{{51}}{{256}}\)
- D \(\frac{3}{{16}}\)
Phương pháp giải:
+) Tính số phần tử của không gian mẫu.
+) Tính số phần tử của biến cố A.
+) Tính xác suất của biến cố A.
Lời giải chi tiết:
Số phần tử của không gian mẫu : \(n\left( \Omega \right) = {2^8} = 256\)
Để không có hai bạn liền kề cùng đứng thì có tối đa 4 bạn đứng.
TH1: Không có ai đứng: Có 1 cách chọn.
TH2: Có 1 bạn đứng:
Số cách chọn: \(8\)cách
TH3: Có 2 bạn đứng:
Nếu chọn bạn đầu tiên là \({A_1}\) thì bạn thứ hai sẽ chọn trong các vị trí: \({A_3},\,{A_4},\,{A_5},\,{A_6},\,{A_7}\)là 5 cách chọn.
Nếu chọn bạn đầu tiên là \({A_i},\,\,i \in \left\{ {2;3;..;8} \right\}\) sau đó chọn bạn thứ hai là \({A_j}\) sao cho \(j > i + 1\)
Khi đó, số cách chọn lần lượt là: 5, 4, 3, 2, 1, 0, 0
\( \Rightarrow \)Tổng số cách chọn là: 5 + 5 + 4 + 3 + 2 + 1 = 20 (cách)
TH4: Có 3 bạn đứng:
Nếu chọn bạn đầu tiên là \({A_1}\) thì bạn thứ hai sẽ chọn trong các vị trí: \({A_3},\,{A_4},\,{A_5},\,{A_6},\,{A_7}\), tương ứng với số cách chọn người thứ ba là: 3, 2, 1, 0, 0.
Tổng: 3 + 2 + 1 = 6 (cách)
Nếu chọn bạn đầu tiên là \({A_i},\,\,i \in \left\{ {2;3;..;8} \right\}\) sau đó chọn bạn thứ hai, thứ ba là \({A_j},\,\,{A_k}\) sao cho \(i + 1 < j;\,\,\,\,j + 1 < k\):
\(i = 2,\,\,\,j = 4 \to k\) có 3 cách chọn
\(i = 2,\,\,\,j = 5 \to k\) có 2 cách chọn
\(i = 2,\,\,\,j = 6 \to k\) có 1 cách chọn
\(i = 2,\,\,\,j > 6 \to k\) có 0 cách chọn
Tổng: 6 cách chọn
\(i = 3,\,\,\,j = 5 \to k\) có 2 cách chọn
\(i = 3,\,\,\,j = 6 \to k\) có 1 cách chọn
\(i = 3,\,\,\,j > 6 \to k\) có 0 cách chọn
Tổng: 3 cách chọn
\(i = 4,\,\,\,j = 6 \to k\) có 1 cách chọn
\(i = 4,\,\,\,j > 6 \to k\) có 0 cách chọn
Tổng: 1 cách chọn
\(i > 4\): Không có cách chọn nào.
\( \Rightarrow \)Tổng số cách chọn là: 6 + 6 + 3 + 1 = 16 (cách)
TH5: Có 4 bạn đứng:
Hoặc là đứng tất ở ô chẵn, hoặc là đứng tất ở ô lẻ \( \to \) 2 cách chọn.
\( \Rightarrow \)Tổng số cách chọn là: 1 + 8 + 20 + 16 + 2 = 47 (cách)
\( \Rightarrow \)Xác suất cần tìm là: \(\frac{{47}}{{256}}\).
Chọn: A







