Câu hỏi
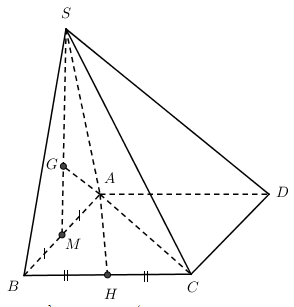
Cho hình chóp SABCD có thể tích là V. ABCD là hình bình hành. G là trọng tâm tam giác SAB. H là trung điểm BC. Tính thể tích SGAH
- A \(\frac{V}{12}\)
- B \(\frac{V}{11}\)
- C \(\frac{V}{10}\)
- D \(\frac{V}{9}\)
Lời giải chi tiết:
+) H là trung điểm của BC Þ \({{S}_{\Delta HAB}}=\frac{{{S}_{\Delta ABC}}}{2}=\frac{{{S}_{ABCD}}}{4}\)
\(\Rightarrow {{V}_{SABH}}=\frac{1}{4}{{V}_{SABCD}}=\frac{1}{4V}\)
+) G là trọng tâm tam giác SAB \(\Rightarrow {{S}_{\Delta SGA}}=\frac{{{S}_{\Delta SAB}}}{3}\)
\(\Rightarrow {{V}_{HSGA}}=\frac{1}{3}{{V}_{HSAB}}=\frac{1}{3}.\frac{V}{4}=\frac{V}{12}\)
Chọn đáp án A
Câu hỏi trước
