Câu hỏi
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau:
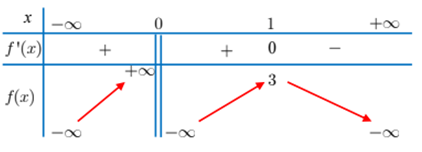
Với các giá trị thực của tham số m, phương trình \(f\left( \left| x \right|+m \right)=0\) có nhiều nhất bao nhiêu nghiệm?
- A 4
- B 5
- C 6
- D 3
Phương pháp giải:
+) Tìm số cực trị tối đa của hàm số \(h\left( x \right)=f\left( \left| x \right|+m \right)\)
+) Hàm số \(h\left( x \right)=f\left( \left| x \right|+m \right)\) có tối đa n cực trị thì phương trình \(h\left( x \right)=f\left( \left| x \right|+m \right)=0\) có tối đa \(n+1\) nghiệm.
Lời giải chi tiết:
Đặt \(h\left( x \right)=f\left( \left| x \right|+m \right)=f\left( \sqrt{{{x}^{2}}}+m \right)\)
\(\Rightarrow h'\left( x \right)=\frac{2x}{2\sqrt{{{x}^{2}}}}f'\left( \left| x \right|+m \right)=\frac{x}{\left| x \right|}f'\left( \left| x \right|+m \right)\)
Số cực trị (nhiều nhất) của hàm số \(y=h\left( x \right)\) là số giá trị của x mà tại đó \(h'\left( x \right)\) không xác định hoặc \(h'\left( x \right)=0\)
+) \(h'\left( x \right)\) không xác định
\( \Leftrightarrow \left[ \begin{array}{l}
\left| x \right| = 0\\
f'\left( {\left| x \right| + m} \right) = 0
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
x = 0\\
\left| x \right| + m = 0\,\,\left( 1 \right)
\end{array} \right.\)
+) \(h'\left( x \right)=0\Leftrightarrow f'\left( \left| x \right|+m \right)=0\Leftrightarrow \left| x \right|+m=1\,\,\left( 2 \right)\)
Phương trình (1) có nhiều nhất 2 nghiệm, phương trình (2) có nhiều nhất 2 nghiệm, do đó hàm số \(y=h\left( x \right)\) có nhiều nhất 5 cực trị. Do đó phương trình \(h\left( x \right)=0\) có nhiều nhất 6 nghiệm.
Chọn C.







