Phương pháp giải:

Công thức tính diện tích mặt cầu: \({{S}_{mc}}=4\pi {{R}^{2}}\)

Lời giải chi tiết:

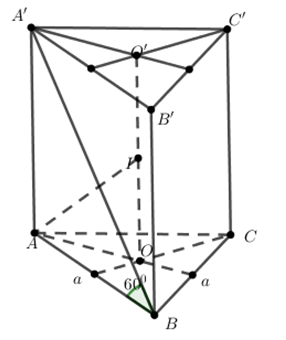
Gọi O và O’ là tâm đường tròn ngoại tiếp 2 đáy như hình vẽ

Ta có: R_cầu = IA = IB = IC = IA’ = IB’ = IC’

Ta có góc giữa đường chéo A’B với mặt đáy (ABC) chính là góc \(\widehat{ABA'}={{60}^{0}}\)

Khi đó ta có: \(AA'=AB.\tan {{60}^{0}}=a.\sqrt{3}\)

Ta có: \(IO=\frac{OO'}{2}=\frac{AA'}{2}=\frac{a\sqrt{3}}{2}\)

Tam giác ABC đều với O là trọng tâm nên \(AO=\frac{2}{3}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3}\)

Xét tam giác vuông AIO ta có:

\(I{{A}^{2}}=I{{O}^{2}}+A{{O}^{2}}={{\left( \frac{a\sqrt{3}}{2} \right)}^{2}}+{{\left( \frac{a\sqrt{3}}{3} \right)}^{2}}=\frac{3{{a}^{2}}}{4}+\frac{3{{a}^{2}}}{9}=\frac{13{{a}^{2}}}{12}\Rightarrow IA=\frac{a\sqrt{39}}{6}\) Vậy diện tích mặt cầu ngoại tiếp hình lăng trụ là:

\(S=4\pi .{{R}^{2}}=4\pi .{{\left( \frac{a\sqrt{39}}{6} \right)}^{2}}=4\pi .\frac{{{a}^{2}}.39}{36}=\frac{13}{3}\pi {{a}^{2}}\)

Chọn A.