Câu hỏi
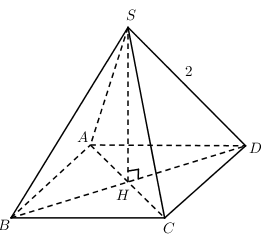
Mặt cầu ngoại tiếp chóp đều \(S.ABCD\) có tất cả các cạnh là \(2\) thì bán kính cầu là:
- A \(1\)
- B \(\sqrt{5}\)
- C \(\sqrt{2}\)
- D \(\sqrt{3}\)
Lời giải chi tiết:
\(+)\,{{\Delta }_{v}}SHB:\,\,SH=\sqrt{S{{B}^{2}}-H{{B}^{2}}}=\sqrt{{{2}^{2}}-{{\left( \sqrt{2} \right)}^{2}}}=\sqrt{2}\)
+) Bán kính cầu ngoại tiếp chóp đều \(S.ABCD\) là: \(R=\dfrac{S{{A}^{2}}}{2h}=\dfrac{S{{A}^{2}}}{2.SH}=\dfrac{{{2}^{2}}}{2.\sqrt{2}}=\sqrt{2}\)
Chọn đáp án C.
Câu hỏi trước
