Câu hỏi
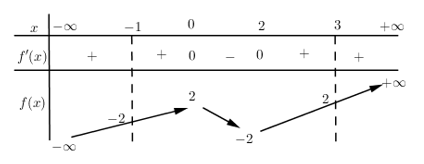
Cho hàm số \(y = f\left( x \right)\)liên tục trên và có bảng biến thiên dưới đây:
Tìm tất cả các giá trị thực của tham số m để phương trình \(f\left( x \right) = f\left( m \right)\) có ba nghiệm phân biệt
- A \(m \in \left( { - 1;3} \right)\backslash \left\{ {0;2} \right\}.\)
- B \(m \in \left[ { - 1;3} \right]\backslash \left\{ {0;2} \right\}.\)
- C \(m \in \left( { - 1;3} \right).\)
- D \(m \in \left( { - 2;2} \right).\)
Phương pháp giải:
Số nghiệm của phương trình \(f\left( x \right) = f\left( m \right)\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và \(y = f\left( m \right)\).
Lời giải chi tiết:
Số nghiệm của phương trình \(f\left( x \right) = f\left( m \right)\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và \(y = f\left( m \right)\) song song với trục hoành.
Để phương trình \(f\left( x \right) = f\left( m \right)\) có ba nghiệm phân biệt thì
\( - 2 < f\left( m \right) < 2 \Rightarrow \left\{ \begin{array}{l} - 1 < m < 3\\m \ne 0;\,\,m \ne 2\end{array} \right. \Rightarrow m \in \left( { - 1;3} \right)\backslash \left\{ {0;2} \right\}\).
Chọn A.