Câu hỏi
Gọi S là tập hợp các giá trị của tham số m để phương trình \(\left| {2{x^4} - 4{x^2} + 1} \right| = m\) có 8 nghiệm phân biệt, tìm S.
- A \(S = \left( {1;2} \right)\).
- B \(S = \left( {0;2} \right)\).
- C \(S = \left( { - 1;1} \right)\).
- D \(S = \left( {0;1} \right)\).
Phương pháp giải:
Số nghiệm của phương trình \(\left| {2{x^4} - 4{x^2} + 1} \right| = m\) bằng số giao điểm của đồ thị hàm số \(y = \left| {2{x^4} - 4{x^2} + 1} \right|\) và đường thẳng \(y = m\).
Lời giải chi tiết:
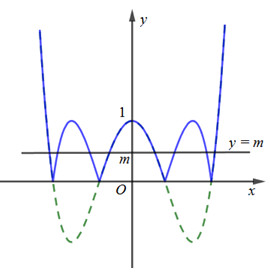
Số nghiệm của phương trình \(\left| {2{x^4} - 4{x^2} + 1} \right| = m\) bằng số giao điểm của đồ thị hàm số \(y = \left| {2{x^4} - 4{x^2} + 1} \right|\) và đường thẳng \(y = m\).
Quan sát đồ thị hàm số ta thấy: Đồ thị hàm số \(y = \left| {2{x^4} - 4{x^2} + 1} \right|\) cắt đường thẳng \(y = m\) tại 8 điểm phân biệt \( \Leftrightarrow 0 < m < 1 \Leftrightarrow m \in \left( {0;1} \right)\)
Vậy, \(S = \left( {0;1} \right)\).
Chọn: D
Câu hỏi trước
