Phương pháp giải:

Gọi \(M\left( {m;\frac{{2m + 1}}{{m + 2}}} \right)\) là điểm thuộc đồ thị hàm số\(y = \frac{{2x + 1}}{{x + 2}}\).

Tính \(d\left( {M;d} \right),\) tìm GTNN của khoảng cách.

Lời giải chi tiết:

Gọi \(M\left( {m;\frac{{2m + 1}}{{m + 2}}} \right)\) là điểm thuộc đồ thị hàm số\(y = \frac{{2x + 1}}{{x + 2}}\).

\( \Rightarrow d\left( {M;d} \right) = \frac{{\left| {3m - \frac{{2m + 1}}{{m + 2}} + 6} \right|}}{{\sqrt {{3^2} + {1^2}} }} = \frac{{\left| {3{m^2} + 4m - 1 + 6m + 12} \right|}}{{\sqrt {10} \left| {m + 2} \right|}} = \frac{1}{{\sqrt {10} }}\left| {\frac{{3{m^2} + 10m + 11}}{{m + 2}}} \right|\)

Xét hàm số \(g\left( m \right) = \frac{{3{m^2} + 10m + 11}}{{m + 2}}\,\,\left( {m \ne  - 2} \right)\) ta có:

\(g'\left( m \right) = \frac{{\left( {6m + 10} \right)\left( {m + 2} \right) - \left( {3{m^2} + 10m + 11} \right)}}{{{{\left( {m + 2} \right)}^2}}} = \frac{{3{m^2} + 12m + 9}}{{{{\left( {m + 2} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}m =  - 1\\m =  - 3\end{array} \right.\)

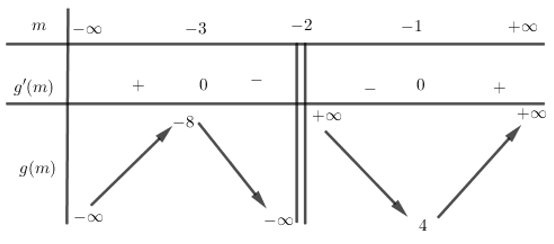
BBT : 

Suy ra\(\left| {g\left( m \right)} \right|\)đạt GTNN tại\(m =  - 1 \Rightarrow a =  - 1,b =  - 1 \Rightarrow 3{a^2} + {b^2} = 4\).

Chọn B.