Phương pháp giải:

Ứng dụng tích phân vào tính diện tích hình phẳng.

Lời giải chi tiết:

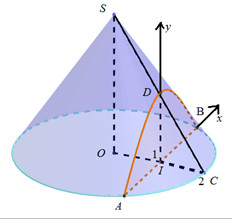
\(DI//SO \Rightarrow \frac{{DI}}{{SO}} = \frac{{IC}}{{OC}} = \frac{1}{2} \Rightarrow DI = \frac{1}{2}.3 = \frac{3}{2}\)

Tam giác OAI vuông tại I \( \Rightarrow IA = \sqrt {O{A^2} - O{I^2}}  = \sqrt {4 - 1}  = \sqrt 3 \)

Gắn hệ trục Oxy như hình vẽ. Trong đó : \(A\left( { - \sqrt 3 ;0} \right),\,\,B\left( {\sqrt 3 ;0} \right),\,\,D\left( {0;\frac{3}{2}} \right)\)

Thiết diện là hình giới hạn bởi parabol đi qua 3 điểm A, B, D và trục hoành.

+) Giả sử parabol có phương trình \((P):y = a{x^2} + bx + c,\,\,a \ne 0\)

\((P)\) đi qua A, B, D \( \Rightarrow \left\{ \begin{array}{l}0 = 3a - \sqrt 3 b + c\\0 = 3a + \sqrt 3 b + c\\\frac{3}{2} = c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a =  - \frac{1}{2}\\b = 0\\c = \frac{3}{2}\end{array} \right.\,\,\, \Rightarrow (P):y =  - \frac{1}{2}{x^2} + \frac{3}{2}\)

+) Diện tích cần tìm là:  \(S = \int\limits_{ - \sqrt 3 }^{\sqrt 3 } {\left| { - \frac{1}{2}{x^2} + \frac{3}{2}} \right|dx}  = \int\limits_{ - \sqrt 3 }^{\sqrt 3 } {\left( { - \frac{1}{2}{x^2} + \frac{3}{2}} \right)dx}  = 2\sqrt 3 \)

Chọn: C