Phương pháp giải:

Cho hai mặt phẳng (

Lời giải chi tiết:

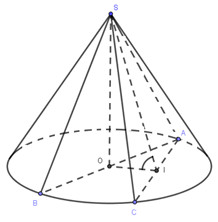
Hình nón đỉnh S, có góc ở đỉnh bằng \({120^0} \Rightarrow \widehat {ASB} = {120^0}\)

\(\Delta SOA\) vuông tại O, \(\widehat {OSA} = \frac{1}{2}\widehat {ASB} = \frac{1}{2}{.120^0} = {60^0}\)

\( \Rightarrow \left\{ \begin{array}{l}SA = \frac{{OA}}{{\sin {{60}^0}}} = \frac{{3R}}{{\frac{{\sqrt 3 }}{2}}} = 2\sqrt 3 R\\SO = \frac{{OA}}{{\tan {{60}^0}}} = \frac{{3R}}{{\sqrt 3 }} = \sqrt 3 R\end{array} \right.\)

Mặt phẳng đi qua S và tạo với đáy góc \({60^0}\), cắt hình nón bởi thiết diện là tam giác SAC.

I là trung điểm AC \( \Rightarrow SI \bot AC\), mà \(SO \bot AC\) (do \(SO \bot \) đáy)  \( \Rightarrow AC \bot (SOI)\) \( \Rightarrow \) Góc tạo bởi (SAB) và mặt đáy:  \(\widehat {SIO} = {60^0}\)

\(\Delta SOI\) vuông tại O \( \Rightarrow SI = \frac{{SO}}{{\sin {{60}^0}}} = \frac{{\sqrt 3 R}}{{\frac{{\sqrt 3 }}{2}}} = 2R\)

\(\Delta SAI\)vuông tại I \( \Rightarrow IA = \sqrt {S{A^2} - S{I^2}}  = \sqrt {{{\left( {2\sqrt 3 R} \right)}^2} - {{\left( {2R} \right)}^2}}  = 2\sqrt 2 R \Rightarrow AC = 2.IA = 4\sqrt 2 R\)

Xét \(\Delta SAC\) có \(SI \bot AC \Rightarrow \)\({S_{SAC}} = \frac{1}{2}SI.AC = \frac{1}{2}.2R.4\sqrt 2 R = 4\sqrt 2 {R^2}\).

Chọn: A