Câu hỏi
Một con lắc lò xo treo thẳng đứng với biên độ 8cm. Khoảng thời gian từ lúc lực đàn hồi cực đại đến lúc lực đàn hồi cực tiểu là T/3, với T là chu kì dao động của con lắc. Tốc độ của vật nặng khi nó cách vị trí thấp nhất 2cm. Lấy g =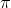 2 m/s2.
2 m/s2.
- A 83,12cm/s
- B 106,45cm/s
- C 87,66cm/s
- D 57,37cm/s
Phương pháp giải:
Sử dụng đường tròn lượng giác và hệ thức độc lập với thời gian của vận tốc và li độ
Lời giải chi tiết:
A = 8cm. Gọi ∆l là độ dãn của lò xo khi vật ở VTCB.
Xét 2 trường hợp:
+ Nếu \(A \le \Delta \ell \) thì vị trí lực đàn hồi cực tiểu ứng với vật ở biên trên, vậy thời gian từ lúc lực đàn hồi cực đại đến khi lực đàn hồi cực tiểu là T/2 => Không phù hợp với bài toán.
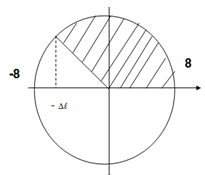
+ Khi \(\Delta \ell \le A\), vật đi từ vị trí lực đàn hồi cực đại ứng với vật ở biên dưới +A đến khi lực đàn hồi cực tiểu ứng với vị trí x = -\(\Delta \ell \), (biểu diễn như hình vẽ) hết thời gian T/3, ứng với góc 1200
Dựa vào hình vẽ ta được \(\Delta \ell = \frac{A}{2} = 4cm = 0,04m \Rightarrow \omega = \sqrt {\frac{g}{{\Delta \ell }}} = 5\pi \left( {rad/s} \right)\)
Khi vật cách vị trí thấp nhất 2cm ứng với x = 6cm, tốc độ của vật là:
\({A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}} \Leftrightarrow {8^2} = {6^2} + \frac{{{v^2}}}{{{5^2}{\pi ^2}}} \Rightarrow |v| = 83,119cm/s\)