Câu hỏi
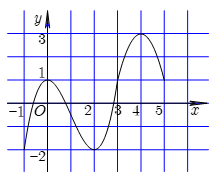
Cho hàm số \(y=f(x)\) có đồ thị của hàm số \(y={f}'(x)\) được cho như hình bên. Hàm số \(y=-2f(2-x)+{{x}^{2}}\) nghịch biến trên khoảng
- A \((-1;\,\,0).\)
- B \((0;\,\,2).\)
- C \((-2;\,\,-1).\)
- D \((-3;\,\,-2).\)
Phương pháp giải:
Tính đạo hàm của hàm hợp, giải bất phương trình dựa vào điều kiện để hàm số nghịch biến và đồ thị hàm số \({f}'\left( x \right)\) để tìm khoảng đơn điệu của hàm số
Lời giải chi tiết:
Xét hàm số \(g\left( x \right)=-2f\left( 2-x \right)+{{x}^{2}},\) có \({g}'\left( x \right)=2{f}'\left( 2-x \right)+2x;\,\,\forall x\in \mathbb{R}.\)
Khi đó \({g}'\left( x \right)<0\Leftrightarrow {f}'\left( 2-x \right)+x<0\Leftrightarrow {f}'\left( 2-x \right)<-\,x\Leftrightarrow {f}'\left( 2-x \right)<2-x-2.\)
Đặt \(t=2-x,\) bất phương trình trở thành: \({f}'\left( t \right)<t-2\)
Dựa vào đồ thị ta thấy rằng \({f}'\left( t \right)<t-2\) với \(1<t<3\Rightarrow \,\,1<2-x<3\Leftrightarrow -\,1<x<1\)
Vậy hàm số đã cho nghịch biến trên khoảng \(\left( -\,1;0 \right).\)
Chọn A