Câu hỏi
Cho hình chóp tam giác đều \(S.ABC\) có cạnh \(AB\) bằng \(a,\) góc tạo bởi hai mặt phẳng \((SAB)\) và \((ABC)\) bằng \({{60}^{0}}.\) Diện tích xung quanh của hình nón đỉnh \(S\) và có đường tròn đáy ngoại tiếp tam giác \(ABC\) bằng
- A \(\frac{\sqrt{7}\pi {{a}^{2}}}{6}.\)
- B \(\frac{\sqrt{7}\pi {{a}^{2}}}{3}.\)
- C \(\frac{\sqrt{3}\pi {{a}^{2}}}{2}.\)
- D \(\frac{\sqrt{3}\pi {{a}^{2}}}{6}.\)
Phương pháp giải:
Xác định góc giữa hai mặt phẳng để tìm chiều cao khối chóp, tính bán kính đường tròn ngoại tiếp đáy và áp dụng công thức tính diện tích xung quanh hình nón
Lời giải chi tiết:
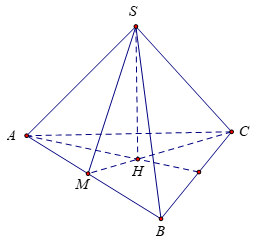
Gọi \(H\) là hình chiếu vuông góc của \(S\) xuống mặt phẳng \(\left( ABC \right).\)
Gọi \(M\) là trung điểm của \(AB\)\(\Rightarrow \left\{ \begin{align} & MH\bot AB \\ & SH\bot AB \\ \end{align} \right.\Rightarrow AH\bot \left( SMH \right)\)
Do đó \(\widehat{\left( \left( SAB \right);\left( ABC \right) \right)}=\widehat{SMH}={{60}^{0}}\)
Lại có \(HM=\frac{1}{3}CM=\frac{a\sqrt{3}}{6}\Rightarrow SH=HM\tan {{60}^{0}}=\frac{a}{2}\)
Bán kính đường tròn ngoại tiếp tam giác ABC là \(R=\frac{a\sqrt{3}}{3}\)
Độ dài đường sinh \(\ell =\sqrt{{{h}^{2}}+{{R}^{2}}}=\frac{a\sqrt{21}}{6}\)
Diện tích xung quanh hình nón là \({{S}_{xq}}=\pi r\ell =\frac{{{a}^{2}}\pi \sqrt{7}}{6}.\)
Chọn A