Phương pháp giải:

Chu vi tam giác ABN: \({C_{ABN}} = AB + AN + BN\).

Mà độ dài AB không đổi \( \Rightarrow {C_{ABN}}\) nhỏ nhất khi và chỉ khi  (\(AN + BN\)) nhỏ nhất.

Lời giải chi tiết:

Nhận xét: Chu vi tam giác ABN: \({C_{ABN}} = AB + AN + BN\).

Mà độ dài AB không đổi \( \Rightarrow {C_{ABN}}\) nhỏ nhất khi và chỉ khi \({\left( {AN + BN} \right)_{\min }}\).

Phương trình đường thẳng Ox: y = 0.

\(A(0;4),\,\,B(3;2)\)

Ta có: \(4.2 > 0 \Rightarrow \) A, B nằm cùng phía so với Ox.

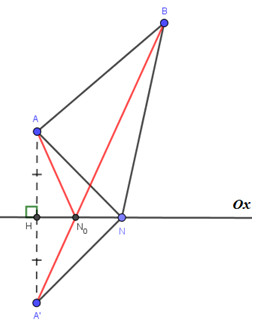
Lấy A’ đối xứng A qua Ox \( \Rightarrow A'(0; - 4)\)

Khi đó, A’ và B nằm khác phía so với Ox và Ox là trung trực của AA’ \( \Rightarrow AN = A'N\)

Ta có:  \(AN + BN = A'N + BN \ge BA'\)

\( \Rightarrow {\left( {AN + BN} \right)_{\min }} = BA'\) khi và chỉ khi \(N = BA' \cap Ox\).

Gọi tọa độ của điểm N khi đó là \(\left( {n;0} \right)\)

\(\overrightarrow {A'N}  = \left( {n;4} \right),\,\,\overrightarrow {BN}  = \left( {n - 3; - 2} \right)\)

A’, N, B thẳng hàng  \( \Leftrightarrow \overrightarrow {A'N} //\,\overrightarrow {BN}  \Leftrightarrow \frac{n}{{n - 3}} = \frac{4}{{ - 2}} \Leftrightarrow  - 2n = 4n - 12 \Leftrightarrow n = 2 \Rightarrow N(2;0)\).

Chọn: B