Phương pháp giải:

Kiểm tra P, Q nằm cùng phía đối với đường thẳng d.

Lấy N tùy ý thuộc \(\Delta \). Ta có:  \(\left| {NP - NQ} \right| \le PQ \Rightarrow {\left| {NP - NQ} \right|_{\max }} = PQ\) khi và chỉ khi \(N = PQ \cap \Delta \).

Lời giải chi tiết:

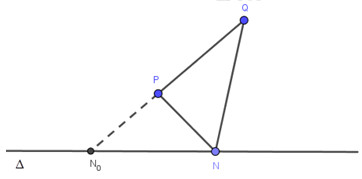
Ta có:

\(\left( {2.1 - 6 - 1} \right)\left( {2.( - 3) - ( - 4) - 1} \right) = ( - 5).( - 3) > 0 \Rightarrow P,\,\,Q\) nằm cùng phía đối với đường thẳng \(\Delta \).

Lấy N tùy ý thuộc \(\Delta \). Ta có:  \(\left| {NP - NQ} \right| \le PQ\)

\( \Rightarrow {\left| {NP - NQ} \right|_{\max }} = PQ\) khi và chỉ khi \(N = PQ \cap \Delta \).

\(\overrightarrow {PQ}  = \left( { - 4; - 10} \right)\), PQ có 1 VTPT là \(\left( {5; - 2} \right)\)

Phương trình đường thẳng PQ là : \(5(x - 1) - 2(y - 6) = 0 \Leftrightarrow 5x - 2y + 7 = 0\)

Tọa độ điểm N để  \(\left| {NP - NQ} \right|\) đạt giá trị lớn nhất là nghiệm của hệ phương trình:

\(\left\{ \begin{array}{l}5x - 2y + 7 = 0\\2x - y - 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  - 9\\y =  - 19\end{array} \right. \Rightarrow N( - 9; - 19)\)

Chọn: A