Câu hỏi
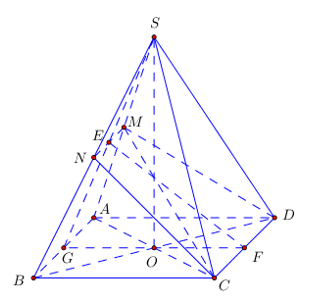
Cho hình chóp đều S.ABCD có đáy là hình vuông cạnh a, M là trung điểm của SA. Biết mặt phẳng (MCD) vuông góc với mặt phẳng (SAB). Thể tích khối chóp S.ABCD là:
- A
\(\frac{{{a^3}}}{{\sqrt 3 }}\)
- B
\(\frac{{{a^3}\sqrt 5 }}{6}\)
- C
\(\frac{{{a^3}\sqrt 5 }}{2}\)
- D \(\frac{{{a^3}\sqrt 3 }}{6}\)
Phương pháp giải:
Gọi O là tâm mặt đáy \( \Rightarrow {V_{S.ABCD}} = \frac{1}{3}SO.{S_{ABCD}}\).
Lời giải chi tiết:
Gọi N là trung điểm của SB ta có \(\left( {MCD} \right) \equiv \left( {MNCD} \right)\).
\( \Rightarrow \left( {MNCD} \right) \bot \left( {SAB} \right)\)
Dễ thấy \(\Delta BCN = \Delta ADM\,\,\left( {c.g.c} \right) \Rightarrow CN = DM\)
\( \Rightarrow MNCD\) là hình thang cân. Gọi E, F lần lượt là trung điểm của MN và CD ta có \(EF \bot MN\)
\( \Rightarrow EF \bot \left( {SAB} \right)\)
Gọi G là trung điểm AB ta có S, E, G thẳng hàng.
Đặt \(SA = SB = SC = SD = x\) ta có \(CN = \frac{{\sqrt {{x^2} + 2{a^2}} }}{2}\)
Dễ dàng tính được \(EF = \frac{{\sqrt {4{x^2} + 7{a^2}} }}{4}\)
Ta có \(EG = \frac{1}{2}SG = \frac{1}{2}\sqrt {{x^2} - \frac{{{a^2}}}{4}} = \frac{{\sqrt {4{x^2} - {a^2}} }}{4}\)
\(\Delta EFG\) vuông tại E \( \Rightarrow E{F^2} + E{G^2} = G{F^2} \Leftrightarrow \frac{{4{x^2} + 7{a^2}}}{{16}} + \frac{{4{x^2} - {a^2}}}{{16}} = {a^2}\)
\( \Leftrightarrow 4{x^2} + 7{a^2} + 4{x^2} - {a^2} = 16{a^2} \Leftrightarrow 8{x^2} = 10{a^2} \Leftrightarrow {x^2} = \frac{{5{a^2}}}{4}\)
Xét tam giác vuông SOB: \(SO = \sqrt {S{B^2} - O{B^2}} = \sqrt {\frac{{5{a^2}}}{4} - \frac{{{a^2}}}{2}} = \frac{{\sqrt 3 a}}{2}\)
Vậy thể tích khối chóp là \({V_{S.ABCD}} = \frac{1}{3}.SO.{S_{ABCD}} = \frac{1}{3}.\frac{{\sqrt 3 a}}{2}.{a^2} = \frac{{\sqrt 3 {a^3}}}{6}\)
Chọn D.