Câu hỏi
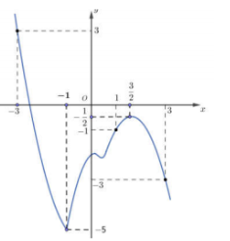
Cho hàm số \(y = f(x)\) có đồ thị hàm số \(f'(x)\) như hình vẽ
Hàm số \(y = f(1 - x) + \frac{{{x^2}}}{2} - x\) nghịch biến trên khoảng
- A \(( - 3;1)\).
- B \(( - 2;0)\).
- C \((1;3)\).
- D \(\left( { - 1;\frac{3}{2}} \right)\).
Lời giải chi tiết:
\(y = f(1 - x) + \frac{{{x^2}}}{2} - x \Rightarrow y' = - f'(1 - x) + x - 1\)
\(\,y' < 0 \Leftrightarrow f'(1 - x) > - (1 - x)\)
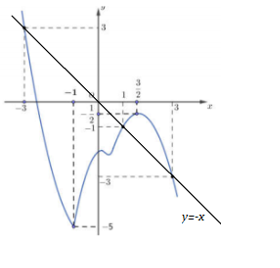
Dựa vào đồ thị hàm số, ta có: Đồ thị hàm số \(f'(x)\) cắt đường thẳng \(y = - x\) tại 3 điểm phân biệt là \(A( - 3;3),\,\,B( - 1;1),\,\,C(3; - 3)\)
\(f'(1 - x) > - (1 - x) \Leftrightarrow \left[ \begin{array}{l}1 - x < - 3\\1 < 1 - x < 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x > 4\\ - 2 < x < 0\end{array} \right.\)
Hàm số \(y = f(1 - x) + \frac{{{x^2}}}{2} - x\) nghịch biến trên các khoảng \(\left( { - 2;0} \right),\,\,\left( {4;\infty } \right)\).
Chọn: B