Phương pháp giải:

\({V_{cau}} = \frac{4}{3}\pi {R^3}\) với R là bán kính khối cầu.

\({V_{non}} = \frac{1}{3}\pi {r^2}h\) với r, h lần lượt là bán kính đáy và chiều cao khối nón.

Lời giải chi tiết:

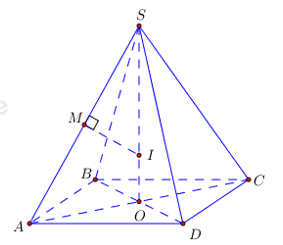
Gọi \(\begin{array}{l}O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right)\\ \Rightarrow \widehat {SA;\left( {ABCD} \right)} = \widehat {\left( {SA;AO} \right)} = \widehat {SAO} = {60^0}\end{array}\)

Gọi M là trung điểm của SA, qua M kẻ đường thẳng vuông góc với SA cắt SO tại I ta có I là tâm khối cầu ngoại tiếp chóp S.ABCD.

Xét tam giác vuông \(SAO\) có

\(SA = \frac{{OA}}{{\cos 60}} = \frac{{\frac{{a\sqrt 2 }}{2}}}{{\frac{1}{2}}} = a\sqrt 2  \Rightarrow SM = \frac{{a\sqrt 2 }}{2}\)

 Xét tam giác vuông SMI có

\(SI = \frac{{SM}}{{\cos {{30}^0}}} = \frac{{\frac{{a\sqrt 2 }}{2}}}{{\frac{{\sqrt 3 }}{2}}} = \frac{{a\sqrt 2 }}{{\sqrt 3 }} = {R_{cau}} \Rightarrow {V_1} = \frac{4}{3}\pi R_{cau}^3 = \frac{{8\sqrt 6 }}{{27}}\pi {a^3}\)

Hình nón ngoại tiếp chóp có chiều cao \(h = SO = AO.\tan 60 = \frac{{a\sqrt 2 }}{2}.\sqrt 3  = \frac{{a\sqrt 6 }}{2}\) và bán kính đáy \(r = AO = \frac{{a\sqrt 2 }}{2}\)

\(\begin{array}{l} \Rightarrow {V_2} = \frac{1}{3}\pi {r^2}h = \frac{{\sqrt 6 }}{{12}}\pi {a^3}\\ \Rightarrow \frac{{{V_1}}}{{{V_2}}} = \frac{{\frac{{8\sqrt 6 }}{{27}}\pi {a^3}}}{{\frac{{\sqrt 6 }}{{12}}\pi {a^3}}} = \frac{{32}}{9}\end{array}\) 

Chọn A.