Câu hỏi
Biết hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có \(M\) và \(m\) lần lượt là GTLN, GTNN của hàm số trên đoạn \(\left[ 0;2 \right]\). Trong các hàm số sau, hàm số nào cũng có GTLN và GTNN tương ứng là \(M\) và \(m\) ?.
- A
\(y = f\left( {\frac{{4x}}{{{x^2} + 1}}} \right)\).
- B \(y=f\left( \sqrt{2\left( \sin x+\cos x \right)} \right)\).
- C
\(y = f\left( {\sqrt {2\left( {{{\sin }^3}x + {{\cos }^3}x} \right)} } \right)\).
- D \(y = f\left( {x + \sqrt {2 - {x^2}} } \right)\).
Phương pháp giải:
Khảo sát các hàm số trong dấu hàm số để xác định khoảng chặn trên, chặn dưới
Lời giải chi tiết:
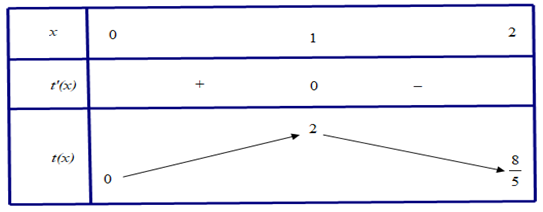
Đặt \(t=\frac{4x}{{{x}^{2}}+1}\) trên \(\left[ 0;2 \right]\). Ta có: \({{{t}'}_{x}}=\frac{-4{{x}^{2}}+4}{{{\left( {{x}^{2}}+1 \right)}^{2}}}\Rightarrow {{{t}'}_{x}}=0\Leftrightarrow x=1\) trên \(\left[ 0;2 \right]\)
Bảng biến thiên:
Dựa vào bảng biến thiên, ta có: \(0\le t\le 2\). Do đó hàm số \(y=f\left( x \right)\) liên tục trên \(\mathbb{R}\) có \(M\) và \(m\) lần lượt là GTLN, GTNN của hàm số trên đoạn \(\left[ 0;2 \right]\) khi và chỉ khi hàm số \(y=f\left( t \right)\) liên tục trên \(\mathbb{R}\) có \(M\) và \(m\) lần lượt là GTLN, GTNN của hàm số trên đoạn \(\left[ 0;2 \right]\).
Chọn A