Phương pháp giải:

Viết phương trình hoành độ giao điểm, cô lập m, khảo sát hàm số biện luận số nghiệm phương trình

Lời giải chi tiết:

Hoành độ giao điểm của đồ thị hàm số \(y={{x}^{3}}+3{{x}^{2}}-9x+2m+1\) và trục \(Ox\) là nghiệm của phương trình \({{x}^{3}}+3{{x}^{2}}-9x+2m+1=0\Leftrightarrow {{x}^{3}}+3{{x}^{2}}-9x+1=-2m\).

Xét hàm số \(f\left( x \right)={{x}^{3}}+3{{x}^{2}}-9x+1\) ta có \({f}'\left( x \right)=3{{x}^{2}}+6x-9\Rightarrow {f}'\left( x \right)=0\Leftrightarrow \left[ \begin{align}& x=1 \\& x=-3 \\\end{align} \right.\).

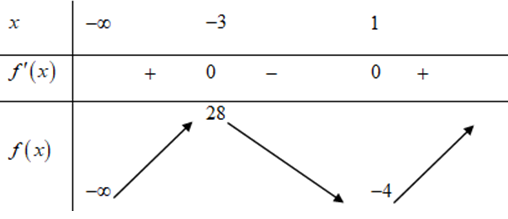
Bảng biến thiên:

Để đồ thị hàm số \(y={{x}^{3}}+3{{x}^{2}}-9x+2m+1\) và trục \(Ox\) có đúng hai điểm chung phân biệt

\(\Leftrightarrow \) phương trình \({{x}^{3}}+3{{x}^{2}}-9x+2m+1=0\) có đúng hai nghiệm phân biệt

\(\Leftrightarrow \) đường thẳng \(y=-2m\) cắt đồ thị hàm số \(f\left( x \right)={{x}^{3}}+3{{x}^{2}}-9x+1\) tại hai điểm phân biệt.

Từ bảng biến thiên ta có điều kiện là: 

\(\left[ \begin{array}{l}
- 2m = - 4\\
- 2m = 28
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
m = 2\\
m = - 14
\end{array} \right. \Rightarrow S = \left\{ {2; - 14} \right\} \Rightarrow T = - \,12.\)

Chọn C