Câu hỏi
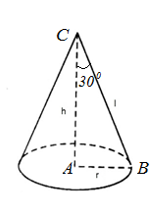
Trong không gian cho tam giác ABC vuông tại A có \(AB=\sqrt{3},\,\,\widehat{ACB}={{30}^{0}}\). Tính thể tích V của khối nón nhận được khi quay tam giác ABC quanh cạnh AC.
- A \(V=5\pi \).
- B \(V=9\pi \).
- C \(V=3\pi \).
- D \(V=2\pi \).
Phương pháp giải:
Thể tích khối nón: \({{V}_{non}}=\frac{1}{3}{{S}_{day}}.h=\frac{1}{3}\pi {{R}^{2}}h\).
Lời giải chi tiết:
Tam giác ABC vuông tại A, \(\widehat{ACB}={{30}^{0}}\Rightarrow AC=\frac{AB}{\tan {{30}^{0}}}=\frac{\sqrt{3}}{\frac{1}{\sqrt{3}}}=3\)
\({{V}_{non}}=\frac{1}{3}\pi {{R}^{2}}h=\frac{1}{3}\pi .{{\left( \sqrt{3} \right)}^{2}}.3=3\pi \)
Chọn: C
Câu hỏi trước
