Câu hỏi
Hai vật nhỏ dao động điều hòa cùng tần số dọc theo hai đường thẳng song song với trục Ox, có phương trình dao động trên trục Ox lần lượt là
\({x_1} = 6\cos (4\pi t - \frac{\pi }{6})(cm)\)
, \(x_2^{} = 6\sqrt 3 \cos (4\pi t + \frac{\pi }{3})(cm)\)
với t tính bằng giây. Khoảng thời gian ngắn nhất kể từ khi hai vật đi ngang qua nhau đến khi khoảng cách giữa hai vật theo phương Ox bằng 6cm là
- A
\(\frac{1}{{12}}s\) - B
\(\frac{1}{6}s\) - C
\(\frac{5}{{24}}s\) - D
\(\frac{1}{{24}}s\)
Phương pháp giải:
sử dụng phương pháp vecto quay
Lời giải chi tiết:
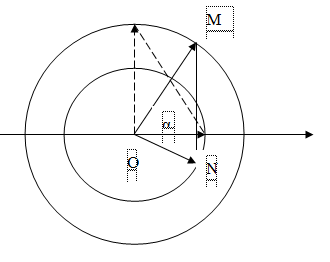
Biểu diễn hai dao động bởi 2 vecto quay chung gốc, có độ dài khác nhau.
Pha ban đầu của hai dao động tạo với nhau goc 900 và không thay đổi khi hai vật chuyển động (do hai vật chuyển động cùng tốc độ góc).
Ta có:
\(MN = \sqrt {O{N^2} + O{M^2}} = 12cm\)
Khi khoảng cách giữa hai vật là 6 cm thì góc tạo bởi MN với Ox là :
\(\cos \alpha = \frac{6}{{12}} = \frac{1}{2} = > \alpha = {60^0}\)
Ta có: thì gian ngắn nhất để khoảng cách giữa hai vật là 6cm chính là thời gian để vecto quay được góc 900 – 600 = 300.
Nên :
\(\Delta t = \frac{{30}}{{360}}.T = \frac{1}{{12}}.\frac{{2\pi }}{\omega } = \frac{1}{{24}}s\)