Câu hỏi
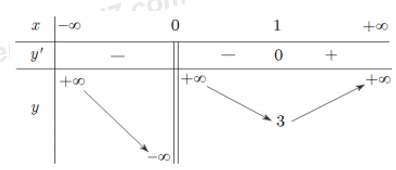
Cho hàm số \(f\left( x \right)\) xác định trên \(R\backslash \left\{ 0 \right\}\) và có bảng biến thiên như hình vẽ. Số nghiệm của phương trình \(3\left| f\left( 2x-1 \right) \right|-10=0\) là:
- A 2
- B 1
- C 4
- D 3
Phương pháp giải:
+) Đặt \(t=2x-1\Rightarrow 3\left| f\left( t \right) \right|-10=0\Leftrightarrow \left| f\left( t \right) \right|=\frac{10}{3}\)
+) Từ BBT của đồ thị hàm số \(f\left( x \right)\) suy ra BBT của đồ thị hàm số \(y=\left| f\left( t \right) \right|\) và biện luận số nghiệm của phương trình.
Lời giải chi tiết:
Đặt \(t=2x-1\Rightarrow 3\left| f\left( t \right) \right|-10=0\Leftrightarrow \left| f\left( t \right) \right|=\frac{10}{3}\)
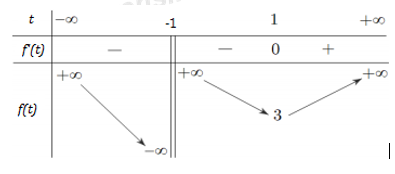
Ta suy ra được BBT của đồ thị hàm số \(f\left( t \right)\) như sau:
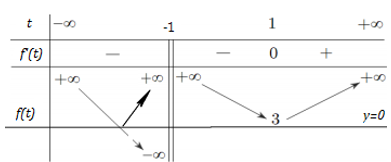
\(\Rightarrow \) BBT của đồ thị hàm số \(y=\left| f\left( t \right) \right|\) :
Số nghiệm của phương trình \(\left| f\left( t \right) \right|=\frac{10}{3}\) là số giao điểm của đồ thị hàm số \(y=\left| f\left( t \right) \right|\) và đường thẳng \(y=\frac{10}{3}\). Dựa vào BBT ta thấy phương trình có 4 nghiệm.
Chọn C.