Câu hỏi
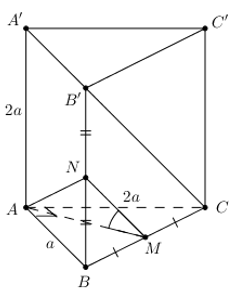
Lăng trụ đứng \(ABC.A'B'C',\,\,AA'=2a,\,\,\Delta ABC\) vuông ở A, \(AB=a,AC=2a,\,\,M\) là trung điểm của BC. Tính \(\widehat{\left( AM;B'C \right)}\)?
- A \(\arccos \frac{1}{\sqrt{5}}\)
- B \(\arccos \frac{7}{12}\)
- C \(\arccos \frac{2}{\sqrt{5}}\)
- D \(\arccos \frac{3}{\sqrt{5}}\)
Lời giải chi tiết:
* Qua M vẽ MN // B’C, \(N\in BB'\Rightarrow \widehat{\left( AM;B'C \right)}=\widehat{AMN}=\widehat{{{M}_{1}}}\).
* Tính
+ Tam giác vuông ABC :
\(BC=\sqrt{4{{a}^{2}}+{{a}^{2}}}=a\sqrt{5}\Rightarrow AM=\frac{BC}{2}=\frac{a\sqrt{5}}{2}\)
+ Tam giác vuông NBA : \(AN=\sqrt{{{a}^{2}}+{{a}^{2}}}=a\sqrt{2}\)
+ Tam giác vuông NBM : \(MN=\sqrt{\frac{5{{a}^{2}}}{4}+{{a}^{2}}}=\frac{3a}{2}.\)
+ \(\cos \widehat{{{M}_{1}}}=\frac{A{{N}^{2}}-M{{N}^{2}}-M{{A}^{2}}}{-2MA.MN}=\frac{2{{a}^{2}}-\frac{9{{a}^{2}}}{4}-\frac{5{{a}^{2}}}{4}}{-2.\frac{a\sqrt{5}}{2}.\frac{3a}{2}}=\frac{1}{\sqrt{5}}\)
Chọn đáp án A.
Câu hỏi trước
