Câu hỏi
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác đều, mặt bên SCD là tam giác vuông cân tại S. Gọi M là điểm thuộc đường thẳng CD sao cho BM vuông góc với SA. Tính thể tích V của khối chóp S.BDM.
- A
\(V=\frac{{{a}^{3}}\sqrt{3}}{16}\) .
- B
\(V=\frac{{{a}^{3}}\sqrt{3}}{24}\).
- C
\(V=\frac{{{a}^{3}}\sqrt{3}}{32}\).
- D \(V=\frac{{{a}^{3}}\sqrt{3}}{48}\).
Phương pháp giải:
- Xác định chân đường cao của đỉnh S đến mặt phẳng đáy.
- Tính thể tích khối chóp : \(V=\frac{1}{3}Sh\)
Lời giải chi tiết:
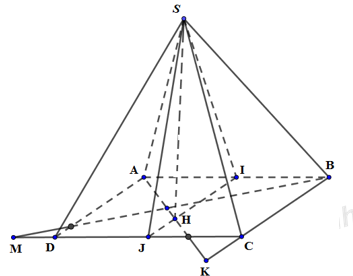
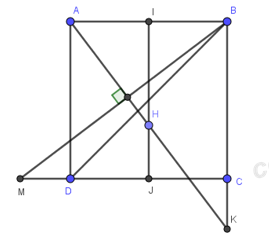
Gọi I, J lần lượt là trung điểm của AB, CD.
Tam giác SAB đều, tam giác SCD cân tại S nên \(SI\bot AB,\,\,SJ\bot CD\)
Mà AB//CD \(\Rightarrow AB,\,\,CD\bot \left( SIJ \right)\)
Dựng \(SH\bot IJ,\,\,(H\in IJ)\Rightarrow SH\bot (ABCD)\) (do \(SH\bot IJ\) và \(SH\subset \left( SIJ \right)\bot CD\))
Trong (ABCD), kẻ \(BM\bot AH,\,\,\left( M\in CD,\,AH\cap BM=T \right)\). Khi đó, điểm M thỏa mãn điều kiện đề bài.
+) \(\Delta SAB\)đều, cạnh a \(\Rightarrow SI=\frac{a\sqrt{3}}{2}\)
+) \(\Delta SCD\)vuông cân tại S, \(CD=a\Rightarrow SJ=\frac{CD}{2}=\frac{a}{2}\)
+) ABCD là hình vuông cạnh a \(\Rightarrow IJ=a\)
Tam giac SIJ có: \(I{{J}^{2}}=S{{I}^{2}}+S{{J}^{2}}\Rightarrow \Delta SIJ\) vuông tại S.
Mà \(SH\bot IJ\Rightarrow S{{I}^{2}}=IH.IJ\Rightarrow {{\left( \frac{a\sqrt{3}}{2} \right)}^{2}}=IH.a\Rightarrow IH=\frac{3a}{4}\)
Và \(\frac{1}{S{{H}^{2}}}=\frac{1}{S{{I}^{2}}}+\frac{1}{S{{J}^{2}}}=\frac{1}{{{\left( \frac{a\sqrt{3}}{2} \right)}^{2}}}+\frac{1}{{{\left( \frac{a}{2} \right)}^{2}}}=\frac{16}{3{{a}^{2}}}\Rightarrow SH=\frac{a\sqrt{3}}{4}\)
Dễ dàng chứng minh \(\Delta AIH\) đồng dạng tam giác \(\Delta BCM\Rightarrow \frac{{{S}_{AIH}}}{{{S}_{BMC}}}={{\left( \frac{AI}{BC} \right)}^{2}}=\frac{1}{4}\Rightarrow {{S}_{BCM}}=4{{S}_{AIH}}=4.\frac{1}{2}.\frac{a}{2}.\frac{3a}{4}=\frac{3{{a}^{2}}}{4}\)
\({{S}_{BDM}}={{S}_{BCM}}-{{S}_{BCD}}=\frac{3}{4}{{a}^{2}}-\frac{1}{2}{{a}^{2}}=\frac{{{a}^{2}}}{4}\)
Thể tích khối chóp S.BDM: \({{V}_{S.BDM}}=\frac{1}{3}.SH.{{S}_{BDM}}=\frac{1}{3}.\frac{a\sqrt{3}}{4}.\frac{{{a}^{2}}}{4}=\frac{\sqrt{3}{{a}^{3}}}{48}\)
Chọn: D