Câu hỏi
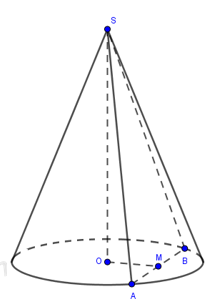
Cho hình nón (N) có đỉnh S, tâm đường tròn đáy là O, góc ở đỉnh bằng \({{120}^{0}}\). Một mặt phẳng qua S cắt hình nón \((N)\) theo thiết diện là tam giác vuông SAB. Biết rằng khoảng cách giữa hai đường thẳng AB và SO bằng 3, tính diện tích xung quanh \({{S}_{xq}}\) của hình nón \((N)\).
- A
\({{S}_{xq}}=36\sqrt{3}\pi \).
- B
\({{S}_{xq}}=27\sqrt{3}\pi \).
- C
\({{S}_{xq}}=18\sqrt{3}\pi \).
- D \({{S}_{xq}}=9\sqrt{3}\pi \).
Phương pháp giải:
Diện tích xung quanh của hình nón: \({{S}_{xq}}=\pi Rl\)
Lời giải chi tiết:
Gọi M là trung điểm AB \(\Rightarrow OM\bot AB\). Mà \(OM\bot SO\) (vì \(SO\) vuông góc với đáy)
\(\Rightarrow OM\) là đoạn vuông góc chung của SO và AB.\(\Rightarrow d(SO;AB)=OM=3\)
Tam giác OMA vuông tại M: \(O{{A}^{2}}=O{{M}^{2}}+M{{A}^{2}}\Rightarrow {{R}^{2}}={{3}^{2}}+M{{A}^{2}}\Rightarrow MA=\sqrt{{{R}^{2}}-9}\)
Tam giác SAB vuông tại A có \(SA=SB\) ( vì \(\Delta SOB=\Delta SOA\,(c.g.c)\))
\(\Rightarrow \Delta SAB\) vuông cân tại S \(\Rightarrow SA=\frac{AB}{\sqrt{2}}=\frac{2AM}{\sqrt{2}}=AM.\sqrt{2}=\sqrt{2{{R}^{2}}-18}\)
(N) có góc ở đỉnh là \({{120}^{0}}\Rightarrow \widehat{ASO}={{60}^{0}}\)
Tam giác SOA vuông tại O:
\(\begin{array}{l}
\sin \widehat {OSA{\mkern 1mu} } = \frac{{OA}}{{SA}} \Rightarrow \sin {60^0} = \frac{R}{{\sqrt {2{R^2} - 18} }} = \frac{{\sqrt 3 }}{2} \Rightarrow 2R = \sqrt 3 .\sqrt {2{R^2} - 18} \\
\Leftrightarrow 4{R^2} = 6{R^2} - 54 \Leftrightarrow {R^2} = 27 \Rightarrow R = 3\sqrt 3
\end{array}\)
\(l=SA=\sqrt{2{{R}^{2}}-18}=\sqrt{2.27-18}=\sqrt{36}=6\)
\({{S}_{xq}}=\pi Rl=\pi .3\sqrt{3}.6=18\pi \sqrt{3}\)
Chọn: C