Câu hỏi
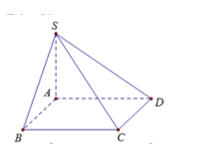
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với mặt đáy (tham khảo hình vẽ bên). Góc giữa hai mặt phẳng (SCD) và (ABCD) bằng
- A
SDA.
- B
SCA.
- C
SCB.
- D ASD.
Phương pháp giải:
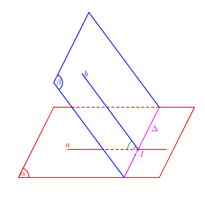
Xác định góc giữa hai mặt phẳng \(\left( \alpha \right),\,\,\left( \beta \right)\):
- Tìm giao tuyến \(\Delta \) của \(\left( \alpha \right),\,\,\left( \beta \right)\).
- Xác định 1 mặt phẳng \(\left( \gamma \right)\bot \Delta \).
- Tìm các giao tuyến \(a=\left( \alpha \right)\cap \left( \gamma \right),b=\left( \beta \right)\cap \left( \gamma \right)\)
- Góc giữa hai mặt phẳng \(\left( \alpha \right),\,\,\left( \beta \right)\): \(\left( \widehat{\left( \alpha \right);\left( \beta \right)} \right)=\left( \widehat{a;b} \right)\).
Lời giải chi tiết:
Ta có: \((SCD)\cap (ABCD)=CD\)
Mà \(CD\bot AD\) (ABCD là hình vuông), \(CD\bot SA\) (vì \(SA\bot (ABCD))\Rightarrow CD\bot (SAD)\)
\((SCD)\cap (SAD)=SD,\,\,(ABCD)\cap (SAD)=AD\Rightarrow \left( \widehat{(SCD),(ABCD)} \right)=\left( \widehat{SD;AD} \right)=\widehat{SDA}\)
Chọn: A