Phương pháp giải:

sử dụng định luật Ôm cho đoạn mạch RLC mắc nối tiếp

Lời giải chi tiết:

Ban đầu mạch RLC nối tiếp nhưng dùng Ampe kế nối tắt qua tụ nên đoạn mạch chỉ còn còn RL. Do I trễ pha so với u một góc \(\frac{\pi }{6}\)

 nên ta có:

\(\tan \frac{\pi }{6} = \frac{{{Z_L}}}{R} = \frac{1}{{\sqrt 3 }} = > R = \sqrt 3 {Z_L}\)

Khi thay thế ampe kế bằng vôn kế thì vôn kế đo giá trị hiệu điện thế hiệu dụng trên tụ C. mạch RLC nối tiếp và điện áp tức thời trên tụ trễ pha

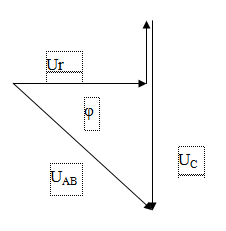
\(\frac{\pi }{4}\) so với điện áp trên đoạn mạch. Ta có giản đồ vecto:

ta có

\(\begin{gathered}
\tan \frac{{ - \pi }}{4} = \frac{{{Z_L} - {Z_C}}}{R} = - 1 \hfill \\
= > {Z_C} - Z{}_L = R \hfill \\
= > {Z_C} = R + {Z_L} = \left( {1 + \frac{1}{{\sqrt 3 }}} \right)R \hfill \\
\end{gathered} \)

mà

\(\begin{gathered}
{U_{AB}} = I.Z = I.\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} = I.\sqrt 2 .R \hfill \\
{U_C} = I.{Z_C} = I.(\frac{1}{{\sqrt 3 }} + 1).R \hfill \\
\end{gathered} \)

Lập tỉ số 

\(\frac{{{U_{AB}}}}{{{U_C}}} = \frac{{\sqrt 2 }}{{\frac{1}{{\sqrt 3 }} + 1}} = > {U_{AB}} = \frac{{\sqrt 2 }}{{\frac{1}{{\sqrt 3 }} + 1}}{U_C} = \frac{{\sqrt 2 }}{{\frac{1}{{\sqrt 3 }} + 1}}.195,19 = 175V\)