Câu hỏi
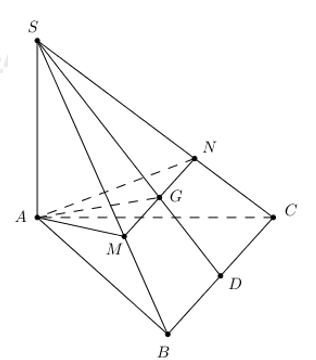
Cho hình chóp S.ABC có đáy là \(\Delta ABC\) vuông cân ở B, \(AC=a\sqrt{2},SA=a\) và \(SA\bot \left( ABC \right)\). Gọi G là trọng tâm \(\Delta SBC\), một mặt phẳng \(\left( \alpha \right)\) đi qua AG và song song với BC cắt SC, SB lần lượt tại M, N. Thể tích khối chóp S.AMN bằng
- A
\(\frac{4{{a}^{3}}}{27}\)
- B
\(\frac{2{{a}^{3}}}{9}\)
- C
\(\frac{4{{a}^{3}}}{9}\)
- D \(\frac{2{{a}^{3}}}{27}\)
Phương pháp giải:
Sử dụng công thức tỉ lệ thể tích: \(\frac{{{V}_{S.AMN}}}{{{V}_{S.ABC}}}=\frac{SA}{SA}.\frac{SM}{SB}.\frac{SN}{SC}\).
Lời giải chi tiết:
Qua G kẻ MN // BC \(\left( M\in SB,N\in SC \right)\Rightarrow \left( \alpha \right)\) cắt SB, SC lần lượt tại M và N.
Gọi D là trung điểm của CD. Ta có \(\frac{SG}{SD}=\frac{2}{3}\).
Theo định lí Ta-let ta có: \(\frac{SM}{SB}=\frac{SN}{SC}=\frac{SG}{SD}=\frac{2}{3}\)
\(\Rightarrow \frac{{{V}_{S.AMN}}}{{{V}_{S.ABC}}}=\frac{SA}{SA}.\frac{SM}{SB}.\frac{SN}{SC}=\frac{4}{9}\)
Ta có \(\Delta ABC\) vuông cân tại B \(\Rightarrow BA=BC=\frac{AC}{\sqrt{2}}=a\)
\(\Rightarrow {{V}_{S.ABC}}=\frac{1}{3}SA.\frac{1}{2}BA.BC=\frac{{{a}^{3}}}{6}\)
Vậy \({{V}_{S.AMN}}=\frac{4}{9}.\frac{{{a}^{3}}}{6}=\frac{2{{a}^{3}}}{27}\)
Chọn D