Phương pháp giải:

Số nghiệm của phương trình \(\left| {{x}^{4}}-5{{x}^{2}}+4 \right|={{\log }_{2}}m\) là số giao điểm của đồ thị hàm số \(y=\left| {{x}^{4}}-5{{x}^{2}}+4 \right|\) và đường thẳng \(y={{\log }_{2}}m\)

Lập BBT của đồ thị hàm số \(\left| {{x}^{4}}-5{{x}^{2}}+4 \right|={{\log }_{2}}m\) và kết luận.

Lời giải chi tiết:

ĐK: \(m>0\).

Số nghiệm của phương trình \(\left| {{x}^{4}}-5{{x}^{2}}+4 \right|={{\log }_{2}}m\) là số giao điểm của đồ thị hàm số \(y=\left| {{x}^{4}}-5{{x}^{2}}+4 \right|\) và đường thẳng \(y={{\log }_{2}}m\)

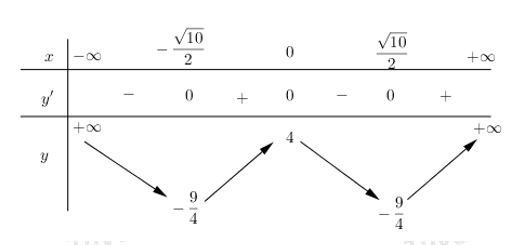
Xét hàm số \(f\left( x \right)={{x}^{4}}-5{{x}^{2}}+4\) có TXĐ: \(D=R\).

\(y'=4{{x}^{3}}-10x=0\Leftrightarrow \left[ \begin{align}  x=0\Rightarrow y=4 \\  x=\pm \frac{\sqrt{10}}{2}\Rightarrow y=-\frac{9}{4} \\ \end{align} \right.\)

BBT:

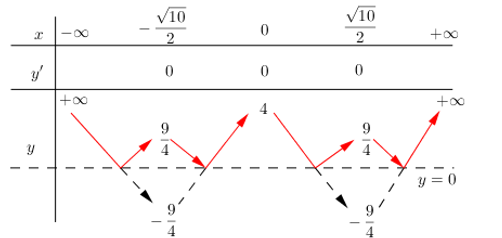
Từ đó ta suy ra được BBT của đồ thị hàm số  \(y=\left| {{x}^{4}}-5{{x}^{2}}+4 \right|\) như sau:

Do đó để phương trình \(\left| {{x}^{4}}-5{{x}^{2}}+4 \right|={{\log }_{2}}m\) có 8 nghiệm thực phân biệt thì đường thẳng \(y={{\log }_{2}}m\) cắt đồ thị hàm số \(y=\left| {{x}^{4}}-5{{x}^{2}}+4 \right|\) tại 8 điểm phân biệt.

\(\Leftrightarrow \) \(0<{{\log }_{2}}m<\frac{9}{4}\Leftrightarrow 1<m<\sqrt[4]{{{2}^{9}}}\).

Chọn D.