Câu hỏi
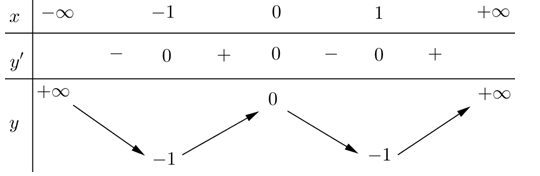
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau:
Tìm tất cả các giá trị của tham số \(m\) để phương trình \(f\left( x \right)=2m\) có nhiều nhất 2 nghiệm.
- A \(m\in \left( -\,\infty ;-\,\frac{1}{2} \right]\cup \left( 0;+\,\infty \right).\)
- B \(m\in \left( 0;+\,\infty \right)\cup \left\{ -\,1 \right\}.\)
- C \(m\in \left( -\,\infty ;-\,1 \right]\cup \left( 0;+\,\infty \right).\)
- D \(m\in \left( 0;+\,\infty \right)\cup \left\{ -\,\frac{1}{2} \right\}.\)
Phương pháp giải:
Phương trình có nhiều nhất n nghiệm thì xảy ra các trường hợp có n nghiệm, có n – 1 nghiệm, … , vô nghiệm, dựa vào bảng biến thiên để biện luận số giao điểm của hai đồ thị hàm số
Lời giải chi tiết:
TH1. Phương trình \(f\left( x \right)=2m\) có 2 nghiệm phân biệt \(\Leftrightarrow \,\,\left[ \begin{array}{l}
2m > 0\\
2m = - \,1
\end{array} \right. \Leftrightarrow \,\,\left[ \begin{array}{l}
m > 0\\
m = - \,\frac{1}{2}
\end{array} \right..\)
TH2. Phương trình \(f\left( x \right)=2m\) có nghiệm duy nhất \(\Leftrightarrow \,\,m\in \varnothing .\)
TH3. Phương trình \(f\left( x \right)=2m\) vô nghiệm \(\Leftrightarrow \,\,2m<-\,1\Leftrightarrow \,\,m<-\,\frac{1}{2}.\)
Vậy \(f\left( x \right)=2m\) có nhiều nhất 2 nghiệm khi và chỉ khi \(m\in \left( -\,\infty ;-\,\frac{1}{2} \right]\cup \left( 0;+\,\infty \right).\)
Chọn A