Phương pháp giải:

Thiết diện là tam giác cân.

Lời giải chi tiết:

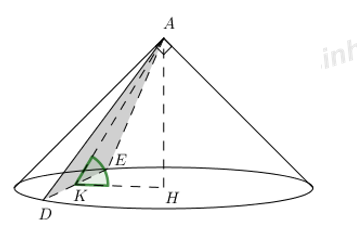
Gọi H là hình chiếu vuông góc của đỉnh A trên mặt phẳng đáy của hình nón.

Thiết diện đi qua trục là tam giác vuông cân cạnh góc vuông bằng 2a \(\Rightarrow 2r=2a\sqrt{2}\Leftrightarrow r=a\sqrt{2}\).

\(\Rightarrow AH=r=a\sqrt{2}\).

Gọi K là trung điểm của DE ta có \(AK\bot DE;\,\,HK\bot DE\Rightarrow \widehat{AKH}={{60}^{0}}\).

Xét tam giác vuông AHK có : \(AK=\frac{AH}{\sin {{60}^{0}}}=\frac{a\sqrt{2}}{\frac{\sqrt{3}}{2}}=\frac{2\sqrt{2}a}{\sqrt{3}};\,\,HK=\frac{AH}{\tan {{60}^{0}}}=\frac{a\sqrt{2}}{\sqrt{3}}\)

Xét tam giác vuông DHK có \(DK=\sqrt{D{{H}^{2}}-H{{K}^{2}}}=\frac{2a}{\sqrt{3}}\Rightarrow DE=\frac{4a}{\sqrt{3}}\).

Vậy \({{S}_{\Delta ADE}}=\frac{1}{2}AK.DE=\frac{1}{2}.\frac{2\sqrt{2}a}{\sqrt{3}}.\frac{4a}{\sqrt{3}}=\frac{4\sqrt{2}{{a}^{2}}}{3}\).

Chọn A.