Câu hỏi
Đặt điện áp xoay chiều u = U0cos(ωt) vào hai đầu đoạn mạch R,L,C mắc nối tiếp, trong đó tụ điện có điện dung C thay đổi. Điều chỉnh C đến giá trị để điện áp hiệu dụng hai đầu tụ điện đạt giá trị cực đại, khi đó điện áp cực đại hai đầu điện trở là 78 V và tại một thời điểm điện áp hai đầu tụ điện, cuộn cảm và điện trở có độ lớn là 202,8 V ; 30 V ; uR. Giá trị uR bằng.
- A 30 V
- B 50 V.
- C 60 V.
- D 40 V.
Phương pháp giải:
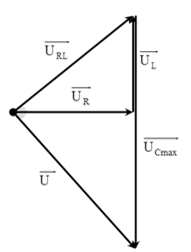
Áp dụng giản đồ vectơ trong mạch điện xoay chiều
Lời giải chi tiết:
Đáp án A.
Biểu diễn vecto các điện áp.
Khi \({{\rm{U}}_{{\rm{Cmax}}}}\) thì điện áp hai đầu mạch vuông pha với điện áp hai đầu đoạn mạch RL
+ Áp dụng hệ thức lượng trong tam giác, ta có: \({\rm{U}}_{0{\rm{R}}}^2{\rm{ = }}{{\rm{U}}_{{\rm{0L}}}}\left( {{{\rm{U}}_{{\rm{0Cmax}}}}{\rm{ - }}{{\rm{U}}_{0{\rm{L}}}}} \right)\)
+ Mặt khác, ta để ý rằng, tại thời điểm t
\(\left\{ \matrix{
{{\rm{u}}_{\rm{C}}} = 202,8 \hfill \cr
{{\rm{u}}_{\rm{L}}} = 30 \hfill \cr} \right.{\rm{V}} \to {{\rm{Z}}_{\rm{C}}} = {{202,8} \over {30}}{{\rm{Z}}_{\rm{L}}} \to {{\rm{U}}_{0{\rm{Cmax}}}} = 6,76{{\rm{U}}_{0{\rm{L}}}}\)
+ Thay vào phương trình hệ thức lượng ta tìm được \({{\rm{U}}_{0{\rm{L}}}} = 32,5{\rm{V}}{\rm{.}}\)
Với hai đại lượng vuông pha uL và uR ta luôn có:
\({\left( {{{{{\rm{u}}_{\rm{L}}}} \over {{{\rm{U}}_{0{\rm{L}}}}}}} \right)^2} + {\left( {{{{{\rm{u}}_{\rm{R}}}} \over {{{\rm{U}}_{0{\rm{R}}}}}}} \right)^2} = 1 \to \left| {{{\rm{u}}_{\rm{R}}}} \right| = {{\rm{U}}_{0{\rm{R}}}}\sqrt {1 - {{\left( {{{{{\rm{u}}_{\rm{L}}}} \over {{{\rm{U}}_{0{\rm{L}}}}}}} \right)}^2}} = 78\sqrt {1 - {{\left( {{{30} \over {32,5}}} \right)}^2}} = 30{\rm{V}}{\rm{.}}\)