Câu hỏi
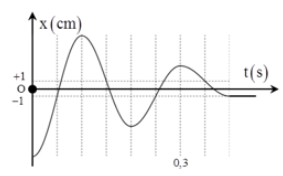
Đồ thị hình bên biểu diễn sự phụ thuộc của li độ theo thời gian của một con lắc lò xo nằm ngang gồm vật có khối lượng m = 100 g và lò xo có độ cứng K. Trong suốt quá trình dao động vật chịu tác dụng của lực cản có độ lớn không đổi bằng 1 N. Chọn gốc toạ độ ở vị trí lò xo không biến dạng, gốc thời gian lúc vật bắt đầu dao động, lấy π2 ≈ 10. Tỷ số giữa tốc độ cực đại và tốc độ trung bình của vật trong suốt quá trình dao động là
- A 0,9π.
- B 0,8π.
- C π.
- D 0,7π.
Phương pháp giải:
Áp dụng công thức của dao động tắt dần của con lắc lò xo
Lời giải chi tiết:
Đáp án B.
+ Từ hình vẽ, ta có \(\Delta {{\rm{l}}_0} = {{{{\rm{F}}_{\rm{c}}}} \over {\rm{k}}} = 0,01{\rm{m}} \to {\rm{k = }}{1 \over {0,01}} = 100{\rm{ N/m,}}\) với \(\Delta {{\rm{l}}_0}\) là độ biến dạng của lò xo tại vị trí cân bằng tạm.
Biên độ dao động của vật trong nửa chu kỳ thứ nhất A1, trong nửa chu kì thứ hai, trong nửa chu kì thứ ba và thứ 4 lần lượt là: A1 = A0 - 1 với A0 là tọa độ ban đầu của vật.
\(\left\{ \matrix{
{{\rm{A}}_2} = {{\rm{A}}_0} - 3 \hfill \cr
{{\rm{A}}_3} = {{\rm{A}}_0} - 5 \hfill \cr
{{\rm{A}}_4} = {{\rm{A}}_0} - 7 = 2 \hfill \cr} \right.{\rm{cm}} \to \left\{ \matrix{
{{\rm{A}}_0} = 9 \hfill \cr
{{\rm{A}}_1} = 8 \hfill \cr
{{\rm{A}}_2} = 6 \hfill \cr
{{\rm{A}}_3} = 4 \hfill \cr
{{\rm{A}}_4} = 2 \hfill \cr} \right.{\rm{cm}}.\)
Tốc độ cực đại của vật trong quá trình dao động \({{\rm{v}}_{{\rm{max}}}} = \omega {{\rm{A}}_1} = 80\pi {\rm{ cm/s}}{\rm{.}}\)
Tốc độ trung bình của vật \({{\rm{v}}_{{\rm{tb}}}} = {{\rm{S}} \over {\rm{t}}} = {{2\left( {{{\rm{A}}_1} + {{\rm{A}}_2} + {{\rm{A}}_3} + {{\rm{A}}_4}} \right)} \over {\rm{t}}} = {{2\left( {8 + 6 + 4 + 2} \right)} \over {0,4}} = 100{\rm{ cm/s}}{\rm{.}}\)
Ta có tỉ số \({{{{\rm{v}}_{\max }}} \over {{{\rm{v}}_{{\rm{tb}}}}}} = 0,8\pi .\)