Câu hỏi
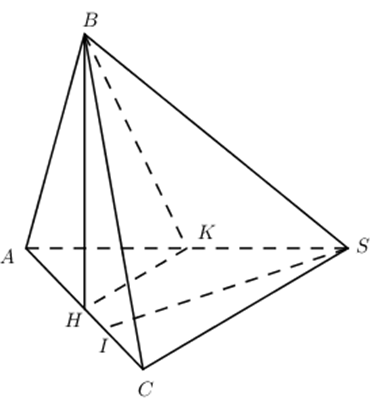
Cho hình chóp \(SABC\) có mặt phẳng \(\left( SAC \right)\) vuông góc với mặt phẳng \(\left( ABC \right),\ SAB\) là tam giác đều cạnh \(a\sqrt{3},\ BC=a\sqrt{3},\) đường thẳng \(SC\) tạo với mặt phẳng \(\left( ABC \right)\) góc \({{60}^{0}}.\) Thể tích của khối chóp \(SABC\) bằng:
- A \(\frac{{{a}^{3}}\sqrt{3}}{3}\)
- B \(\frac{{{a}^{3}}\sqrt{6}}{2}\)
- C \(\frac{{{a}^{3}}\sqrt{6}}{6}\)
- D \(2{{a}^{3}}\sqrt{6}\)
Phương pháp giải:
+) Sử dụng phương pháp đổi đỉnh. Chóp S.ABC có đỉnh B và đáy SAC.
+) Chứng minh tam giác SAC vuông tại S.
+) Xác định góc giữa SC và (ABC).
+) Sử dụng công thức tính thể tích \(V=\frac{1}{3}Bh\).
Lời giải chi tiết:
Có \(AB=BC=a\sqrt{3}\Rightarrow \Delta ABC\) cân tại B.
Gọi H là trung điểm của AC ta có \(BH\bot AC\) \(\left\{ \begin{align} & \left( ABC \right)\bot \left( SAC \right) \\ & \left( ABC \right)\cap \left( SAC \right)=AC \\ & \left( ABC \right)\supset BH\bot AC \\ \end{align} \right.\Rightarrow BH\bot \left( SAC \right)\Rightarrow BH\bot SA\,\,\,\left( 1 \right)\)
Gọi K là trung điểm của SC, do tam giác SAB đều \(\Rightarrow BK\bot SA\,\,\,\left( 2 \right)\)
Từ (1) và (2) \(\Rightarrow SA\bot \left( BHK \right)\Rightarrow SA\bot HK\).
Lại có HK là đường trung bình của tam giác SAC \(\Rightarrow HK//SC\Rightarrow SA\bot SC\Rightarrow \Delta SAC\) vuông tại S.
Trong (SAC) kẻ \(SI\bot AC\), tương tự ta có \(SI\bot \left( ABC \right)\Rightarrow \widehat{\left( SC;\left( ABC \right) \right)}=\widehat{\left( SC;IC \right)}=\widehat{SCI}={{60}^{0}}\)
Xét tam giác vuông SAC có \(SC=AC.\cot 60=a\sqrt{3}.\frac{1}{\sqrt{3}}=a\Rightarrow AC=\sqrt{{{a}^{2}}+3{{a}^{2}}}=2a\). \(\Rightarrow {{S}_{SAC}}=\frac{1}{2}SA.SC=\frac{1}{2}a\sqrt{3}.a=\frac{{{a}^{2}}\sqrt{3}}{2}\)
Có H là trung điểm của AC \(\Rightarrow AH=\frac{1}{2}AC=a\Rightarrow BH=\sqrt{B{{A}^{2}}-A{{H}^{2}}}=\sqrt{3{{a}^{2}}-{{a}^{2}}}=a\sqrt{2}\). Vậy \({{V}_{S.ABC}}=\frac{1}{3}BH.{{S}_{SAC}}=\frac{1}{3}a\sqrt{2}.\frac{{{a}^{2}}\sqrt{3}}{2}=\frac{{{a}^{3}}\sqrt{6}}{6}\).
Chọn C.