Câu hỏi
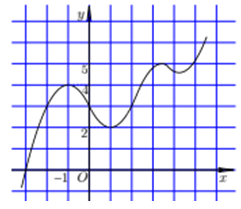
Cho hàm số \(y=f\left( x \right)\) có đồ thị như hình vẽ bên. Tìm số giá trị nguyên của m để phương trình \(f\left( {{x}^{2}}-2x \right)=m\) có đúng 4 nghiệm thực phân biệt thuộc đoạn \(\left[ -\frac{3}{2};\frac{7}{2} \right]\).
- A 1
- B 4
- C 2
- D 3
Phương pháp giải:
+) Đặt \(t\left( x \right)={{x}^{2}}-2x\), tìm miền giá trị của t.
+) Tìm điều kiện tương đương số nghiệm của phương trình \(f\left( t \right)=m\) để phương trình \(f\left( {{x}^{2}}-2x \right)=m\) có đúng 4 nghiệm thực phân biệt thuộc đoạn \(\left[ -\frac{3}{2};\frac{7}{2} \right]\)
Lời giải chi tiết:
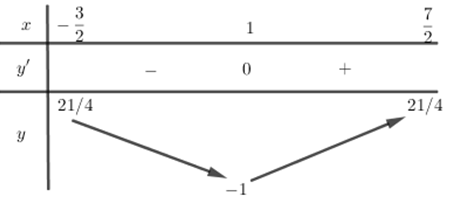
Xét hàm số \(t\left( x \right)={{x}^{2}}-2x\) trên \(\left[ -\frac{3}{2};\frac{7}{2} \right]\) ta có \(t'\left( x \right)=2x-2=0\Leftrightarrow x=1\in \left[ -\frac{3}{2};\frac{7}{2} \right]\)
BBT : \(\Rightarrow t\in \left[ -1;\frac{21}{4} \right]\) Với \(t=-1\) thì ứng với mỗi giá trị của t thì có 1 nghiệm x và với \(t\in \left( -1;\frac{21}{4} \right]\) thì ứng với mỗi giá trị của t có 2 nghiệm x phân biệt.
Do đó để phương trình ban đầu có 4 nghiệm phân biệt thuộc đoạn \(\left[ -\frac{3}{2};\frac{7}{2} \right]\) thì phương trình \(f\left( t \right)=m\) có 2 nghiệm phân biệt thuộc \(\left( -1;\frac{21}{4} \right]\).
\(\Rightarrow m\in \left( 2;4 \right)\cup \left( a;5 \right]\) với \(a\in \left( 4;5 \right)\) \(\Rightarrow \) Có 2 giá trị nguyên của m thỏa mãn là m = 3 và m = 5.
Chọn C.